Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 7.Problemas - Ex. 96
Se cada segmento do cabo puder suportar uma tração máxima de , determine a maior carga que pode ser aplicada.
Passo 1
O problema quer que a gente encontre a maior força que pode ser aplicada sem nenhuma das trações ultrapassar .
A gente vai começar calculando o momento em , que é:
Agora, vamos analisar as forças, primeiro no eixo :
No eixo fica:
Usando essas equações a gente usa a tesão máxima, para calcular os outros termos:
Passo 2
Então vamos analisar as forças da junta , assim:
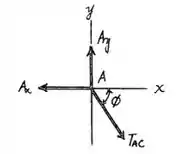
Que é menor do que , então, tá tudo certo.
Então, analisamos também a junta , vou deixar essa pra você pra poupar tempo, mas eu sei que você consegue, você vai encontrar:
Que também é menor que . Então, a maior tensão é mesmo a de , vamos usar ela como a tensão máxima mesmo.
Passo 3
E por fim, vamos calcular a força :