Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 118

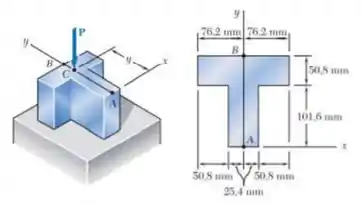
uma força vertical P de intensidade 89   k N é aplicada a um ponto C localizado no eixo de simetria da seção transversal de uma coluna curta. Sabendo que y z = 127 m m , determine:

  1. A tensão no ponto A;
  2. A tensão no ponto B.
  3. A localização da linha neutra.

Passo 1

Fala galerinha, nosso objetivo com essa questão é determinar as tensões e também a LN levando em conta que temos uma carga de compressão que vai mover a LN que aprendemos a calcular. Para isso, precisamos lembrar da nossa equação de tensão, que é dada por:

σ x = - P A - M y I

Antes de calcularmos qualquer coisa, precisamos da nossa LN, e assim podemos ver isso no próximo passo.

Passo 2

Precisamos da LN para determinarmos tudo que precisamos, momento fletor, o valor de y e o valor do momento de inércia, com isso podemos usar a seguinte fórmula para a LN.

y - = A 1 y - 1 + A 2 y - 2 A 1 + A 2

A nossa seção é dada por:

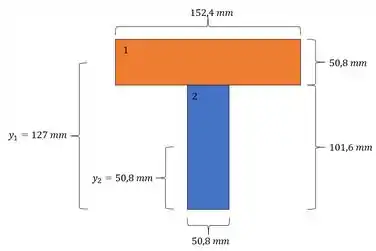
Substituindo teremos que:

y - = 15 2,4 × 50,8 × 127   + 101,6 × 50,8 × 50,8   152,4 × 50,8 + 101,6 × 50,8

y - = 96,52   m m  

Passo 3

Agora que temos a LN, podemos determinar o momento de inércia

  • I

    • Para ele precisamos fazer a seguinte relação.

    I = ( I 1 + A 1 d 1 2 ) + I 2 + A 2 d 2 2

    I = 152,4 × 50,8 3 12 + 15 2,4 × 50,8 × 30,48 2 + 50,8 × 101,6 3 12 + 101,6 × 50,8 × 45,72 2

    I = 24085925   m m 4

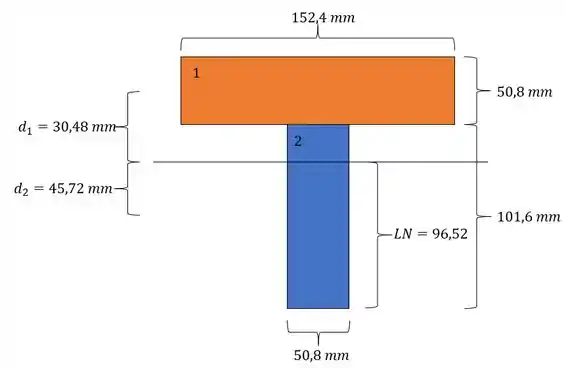
    Agora só precisamos determinar os valores de y, sendo assim teremos que ver o próximo passo.

    Passo 4

    Tendo o valor de y precisamos usar a tensão, sendo assim teremos que:

  • y - positivo e negativo

E para calculo de momentos fletores temos que detemrinar a excentricidade, sendo assim teremos que:

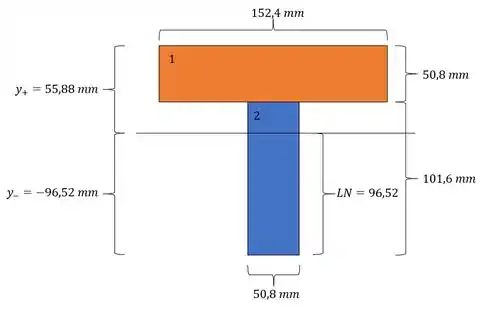
E para o cálculo do momento temos que usar a nossa excentricidade, sabemos que a nossa carga é aplicada a um distancia y z da base:

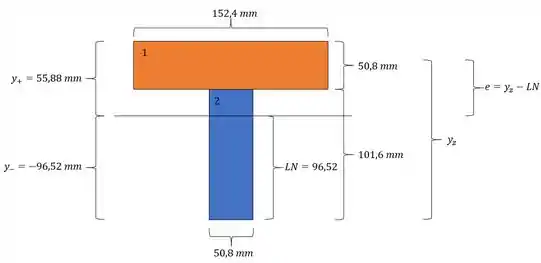
Assim temos que o nosso momento vai ser calculado pela seguinte equação.

M = P   x   e

M = P × y z - L N

Substituindo nas tensões teremos que:

σ x = - P A - M y I

σ x = - P A - P × y z - L N y I

E pelo enunciado sabemos que:

P = 89   k N = 89000   N

A = 12903,2   m m 2

I = 24085925   m m 4

y z = 127   m m

L N = 96,52   m m

Calculando assim a tensão em B primeiro, temos que usar y + = 55,88   m m , assim temos que:

σ B = - 89000 12903,2 - 89000 × 127   - 96,52 × 55,88 24085925 = 13,2 N m m 2 = - 13,2   M P a

Calculando assim a tensão em A primeiro, temos que usar y - = - 96,52   m m , assim temos que:

σ A = - 89000 12903,2 - 89000 × 127   - 96,52 × - 96,52 24085925 = 3,97 N m m 2 = 3,97   M P a

E assim resolvemos o nosso item A) e B).

Passo 4

Para determinarmos a posição da nossa LN é muito simples, porque basta apenas igualarmos a nossa tensão a zero, assim temos que:

0 = - P A - M y I

P A = - M y I

y = - P I A M

E sabemos que o momento é dado pela seguinte equação:

M = P × y z - L N

y = - P I A P y z - L N

y = - I A y z - L N

Sabemos que:

A = 12903,2   m m 2

I = 24085925   m m 4

y z = 127   m m

L N = 96,52   m m

y = - 24085925 12903,2 127 - 96,52

y = - 24085925 12903,2 127 - 96,52 = - 61,2   m m

E essa distância é dada com relação a nossa LN original, e como é negativa, é para baixo, assim temos que:

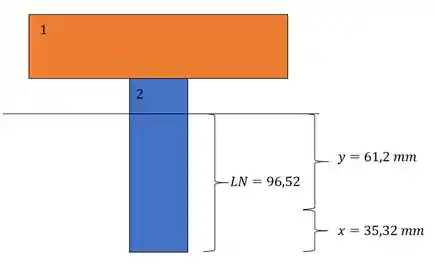
Assim, a distância da LN, com relação a base da peça, é dado por:

x = 35,3   m m

Resposta

  1. σ A = 3,97   M P a

  2. σ B = - 13,2   M P a

  3. x = 35,3   m m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o componente de máquinas e o carregamento mostrado, determinar a tensão no ponto A quando: (b) h = 65m m ;
Mostrar que, se uma viga maciça retangular é curvada por um momento aplicado no plano que contém uma das diagonais da seção retangular mostrada, a superfície neutra será ao longo da outra diagonal.
Para a barra curva e o carregamento mostrado, determinar a máxima tensão de compressão quando: (b) r = 15m m ;
Para o componente de máquinas e o carregamento mostrado, determinar a tensão no ponto A quando: (a) h = 50m m ;
Uma viga com a seção transversal mostrada está submetida a um momento M 0 , que atua em um plano vertical. Determinar o maior valor permissível do momento fletor M 0 , se a máxima tensão na viga não e