Mostrar que, se uma viga maciça retangular é curvada por um momento aplicado no plano que contém uma das diagonais da seção retangular mostrada, a superfície neutra será ao longo da outra diagonal.
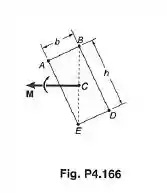
Passo 1
Queremos provar que a linha neutra passa por . Para isso a gente precisa descobrir os momentos de inércia dos eixos principais:
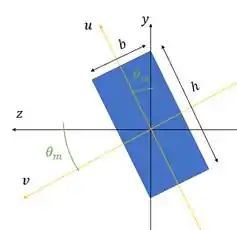
A gente também precisa de uma relação para . Olhando na figura, vemos que o cateto oposto do ângulo vale e o adjacente . Então:
Passo 2
Agora a gente tem que descobrir onde é a linha neutra. A gente descobre isso pela fórmulinha:
Onde é o ângulo entre a linha neutra e o eixo . Substituindo os nossos dados:
Agora é só a gente achar o ângulo que tem como cateto oposto e como cateto adjacente. A gente percebe pelo resultado da tangente que esse ângulo quando somado a dá .
Então nossa linha neutra está nessa posição:
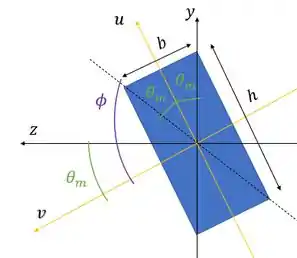
Passando pela outra diagonal. Ufa!
Resposta
Prova nos passos