Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 190
As formas para um pequeno muro de contenção de concreto são mostradas em seção. Existe uma braçadeira BC para cada 1,5 m de comprimento de parede. Supondo que as juntas em A, B e C funcionem como conexões articuladas, calcule a compressão em cada chave BC. O concreto úmido pode ser tratado como um líquido com densidade de 2.400 kg/m3.
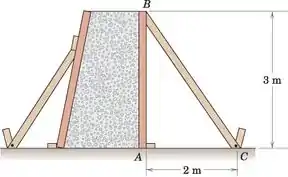
Passo 1
Nesta tarefa, precisamos determinar a força FCB atuando no ponto B.
O comprimento da parede é de 1,5 m
A densidade da coisa vermelha na imagem é 2.400 kg/m3.
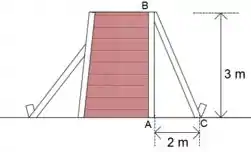
A área ABC é
A pressão por unidade é
A força R é
O ângulo CBA é
Passo 2
E finalmente vamos determinar a força FCB através do equilíbrio de momento no ponto A.
Resposta
Exercícios de Livros Relacionados
A seção transversal mostrada representa um corpo de revolução, em torno do eixo z , de uma peça fabricada em ferro fundido. Calcule sua massa m .
O tampão de ferro fundido fecha o tubo de drenagem de um tanque aberto de água doce, que está cheio até uma altura de 20f t . Determine a força trativa T necessária para remover o tampão sobre o burac
A barra AB de comprimento de 500 mm está conectada por juntasrotuladas aos colares A e B, que deslizam ao longo das duas barrasmostradas na figura. Sabendo que o colar B aproxima-se do ponto Ea uma ve
A montagem consiste em quatro barras cortadas de uma mesma barra original. O elemento curvo é um arco circular de raio b . Determine as coordenadas y e z do centro de massa desta montagem.
Construa os diagramas de cortante e de momento para a viga, que sustenta a carga uniforme de 50l b por metro do comprimento da viga, distribuída ao longo da sua seção média. Determine o momento fletor