Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 186

A câmara de mergulho submersível tem uma massa total de 6,7 mg, incluindo pessoal, equipamento e lastro. Quando a câmara é baixada a uma profundidade de 1,2 km no oceano, a tensão do cabo é de 8 kN. Calcule o volume total V deslocado pela câmara.

Passo 1

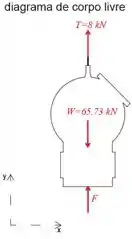
Primeiro, vamos isolar e desenhar o diagrama de corpo livre da câmara de mergulho com seu peso, tensão do cabo e força de flutuação atuando nele.

Observe que o peso da câmara é:

W = m g

W = 6.7 ∙ 9.81 = 65.73   kN

Passo 2

Pela equação da soma das forças na direção y para zero, podemos determinar a força de empuxo F

∑ F y = 0

F + 8 - 65.73 = 0

F = 65.73 - 8

F = 57.73   kN

Como dito no problema anterior, a força de empuxo é igual ao peso da água, que é igual ao produto da densidade, gravidade e volume da água.

F = ρ w ∙ g ∙ V

Passo 3

A partir daqui, podemos expressar o volume da câmara como:

V = F ρ w ∙ g

A densidade da água do oceano (água salgada) é ρ w   =   1,03   Mg/ m 3 , enquanto a gravidade e a força de empuxo são conhecidas.

V = 57.73 1.03 ∙ 9.81

⇒                     V = 5.71   m 3

Resposta

V = 5.71   m 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um comprimento de cabo com massa de 1,2 kg / m deve ter uma curvatura de 2,4 m quando suspenso dos dois pontos A e B na mesma linha horizontal de 10 m de distância. Para fins de comparação, determine
O cilindro de concreto sólido com 6 pés de comprimento e 4 pés de largura diâmetro é apoiado em uma posição semi-submersa em água doce por um cabo que passa sobre um polia em A. Calcule a tensão T no
A seção transversal de um tanque de água doce com um fundo inclinado é mostrado. Uma porta retangular de 1,6 m por 0,8 m (normal ao plano da figura) no fundo do tanque é articulado em A e é aberto con
Os lados de uma calha de água doce em forma de V, mostrado na seção, são articuladas ao longo de sua interseção comum através de O e são apoiadas em cada lado por escoras verticais articuladas em cada
Determine a força total R exercida sobre a janela triangular pela água doce no tanque. O nível da água coincide com o topo da janela. Determine, também, a distância H , desde R até o nível da água.