Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 235
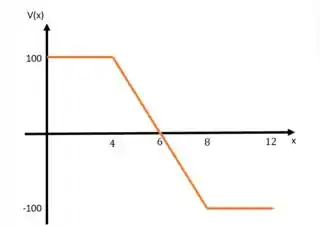
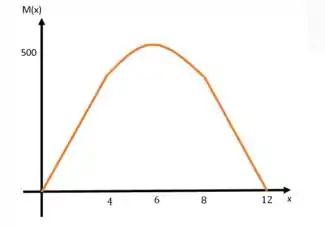
Construa os diagramas de cortante e de momento para a viga, que sustenta a carga uniforme de por metro do comprimento da viga, distribuída ao longo da sua seção média. Determine o momento fletor máximo e sua posição.
Passo 1
E aíí galera
Olha só, pra começar, vamos calcular a força externa sobre a viga:
Então, levando em conta a simetria do desenho, cada um dos apoios deve fazer uma força de para cima, correto?
Passo 2
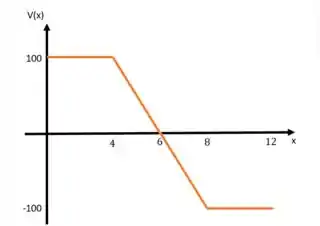
Dado que a viga é simétrica, vamos dividir em apenas duas regiões: a primeira vai de até e a segunda de até . Depois disso, é tudo simétrico.
Na região , temos
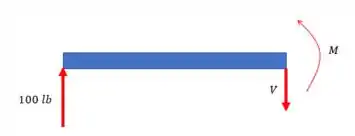
Como estamos em equilíbrio, temos:
E:
Passo 3
Para , temos o diagrama:
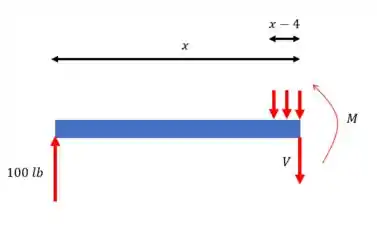
E aí:
E pelo equilíbrio, temos:
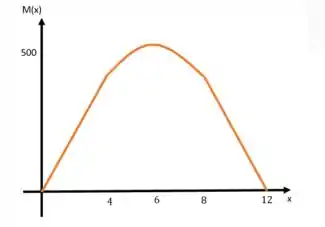
E para encontrar o momento, temos
Passo 4
Temos
A partir de , vamos espelhar esse comportamento (pela simetria), então, temos:
E é isso aí, arrasamos!!
Resposta
