Os grampos na fileira AB contida no grampeador estão colados de modo que a tensão de cisalhamento máxima que a cola pode suportar é máx= 84kPa. Determine a força mínima F para estrair o grampo da fileira por cisalhamento e permitir que ele saia sem deformação pela fenda em C. As dimensões externas do grampo são mostradas na figura, e a espessura é 1,25 mm. Considere que todas as outras partes são rígidas e despreze o atrito.
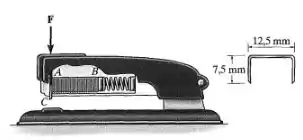
máx
= 84 kPa. Determine a força mínima F que deve ser aplicada ao êmbolo para extrair um
Passo 1
Olá, querido! Cê tá bem?
Então, ele quer saber a força necessária para cortar um grampo. Sabe, quando você vai usar o grampeador, aí ele destaca um pedacinho de grampo. Ele quera força que o grampo faz que realiza esse corte.
Cara, basicamente, o corte é causado por uma força paralela a seção, certo? Então é uma força de cisalhamento. E aí a força gera uma tensão de cisalhamento na seção do objeto e aí o corte acontece. Essa tensão vai ser dada por
Ele diz que essa tensão necessária vale . Então se a gente achar a área da seção que é paralela a força , conseguimos encontrar assim:
Vamo!
Passo 2
A seção do grampo que vai sofrer o corte é a mostrada na figura do enunciado. A gente pode dividir ela em retângulos:
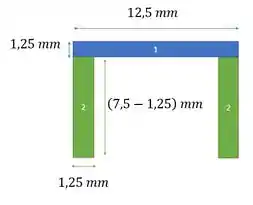
A área dessa seção fica
Passo 3
Agora podemos usar a fórmulinha da tensão e achar :
Substituindo os dados: