Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 39
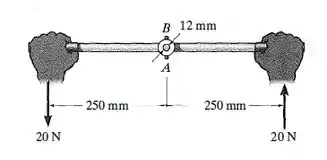
A alavanca está presa ao eixo fixo por um pino cônico AB, cujo diâmetro médio é 6 mm. Se um binário for aplicado à alavanca, determine a tensão de cisalhamento média no pino entre ele e a alavanca.
Passo 1
Oláaaaa, querido! Cê está bem? Torcendo para que sim!
Então, essa figur está um pouco confusa, sabe? Vamos analisar ela com cuidado. Temos uma pessoa aplicando um binário em um eixo. Só que no eixo temos um pino que impede que a rotação aconteça. Como?
Bem, o pino aplica um binário no eixo de rotação que se equilibra como binário que a pessoa aplicou. Algo assim:
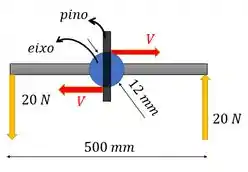
O binário de tenta girar o eixo azul, mas o pino que passa por dentro desse eixo azul é fixo na posição dele, então ele reage aplicando duas forças na borda do eixo, gerando outro binário. Ambos os binários são em relação ao centro do eixo azul.
E aí essas forças , vão gerar uma força interna de cisalhamento no pino. E isso vai gerar uma tensão de cisalhamento nele. E é isso que a gente quer descobrir: a tensão de cisalhamento no pinto. Bora ver como fazer isso!
Passo 2
A gente precisa do valor de para calcular a tensão. A gente pode achar esse cara fazendo o equilíbrio de momentos em relação ao eixo de rotação.
O momento causado por um binário é o produto entre o módulo de uma força e a distância entre forças. O momento causado pelo binário de vai ser:
Positivo porque a gente vai considerar o sentido anti-horário positivo. Já o causado por vai ser
Negativo porque ele está no sentido horário. Pelo equilíbrio, vamos ter:
Passo 3
Então a gente acabou de achar . E queremos a tensão de cisalhamento. Mas antes de calcular essa tensão, precisamos ver o cisalhamento que a gente tem é duplo ou simples. Vamos olhar nosso pino mais de perto. Dar aquele zoom esperto:
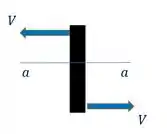
Temos apenas o par de forças que se cancelam atuando nele. Vamos fazer uma seção nele para achar a força de cisalhamento interna
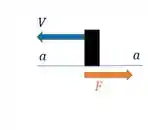
Percebe que a força de cisalhamento interna vai ser, pelo equilíbrio desse pino cortado,
Ou seja, temos um cisalhamento simples. E a tensão de cisalhamento vai ser
Passo 4
Nosso problema está quase terminando, resta-nos calcular a área da seção de cisalhamento que é a área do pino com seção circular
Assim, teremos que a tensão de cisalhamento média será dada por:
Lembrando que teremos