Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 53
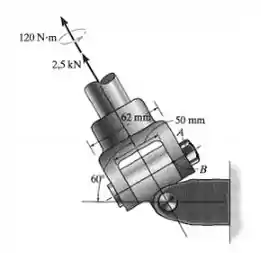
O garfo está sujeito a força e a um binário. Determine a tensão de cisalhamento média no parafuso que age nas seções transversais que passam por A e B. O parafuso tem 6 mm de diâmetro. Dica: O binário sofre a resistência de um conjunto de forças desenvolvidas nas hastes do parafuso.
Passo 1
Vamos, primeiramente, desenhar o DCL:
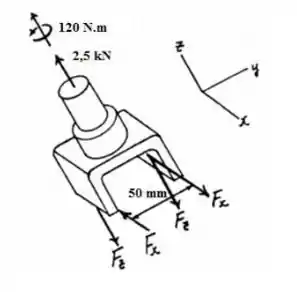
Podemos observar na figura do enunciado que o ponto A está fora da zona que sofre cisalhamento e portanto, possui tensão nula.
Já para o ponto B, temos que aplicar as equações de equilíbrio:
Sabemos que a força em B será a soma das forças em x e z:
Passo 2
Calculando a área do parafuso:
mm²
Passo 3
Calculando a tensão cisalhante:
Resposta
Exercícios de Livros Relacionados
A estrutura está sujeita a carga de 1k N . Determine a tensão de cisalhamento média no parafuso em A em função do ângulo da barra θ . Represente essa função em gráfico para 0 ≤ θ ≤ 90 ° e indique os v
A viga é apoiada por um pino em A e um elo curto B C . Se P=15k N , determine a tensão de cisalhamento média desenvolvida nos pinos em A ,BeC . Todos os pinos estão sujeitos a cisalhamento duplo, como
A estrutura de dois elementos está sujeita à carga distribuída mostrada. Determine a maior intensidade w da carga uniforme que pode ser aplicada à estrutura sem que a tensão normal média ou a tensão d
O parafuso longo passa pela chapa de 30 m m de espessura.Se a força na haste do parafuso for 8 k N , determine a tensão normal média na haste, a tensao de cisalhamento média ao longo da área cilíndric
O punção circular B exerce uma força de 2k N na parte superior da chapa A . Determine a tensão de cisalhamento média na chapa provocada por essa carga.