Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 60
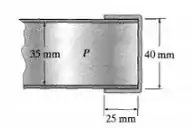
O tampão é utilizado para vedar a extremidade do tubo cilíndrico que está sujeito a uma pressão interna p = 650Pa. Determine a tensão de cisalhamento média que a cola exerce sobre os lados do tubo necessária para manter o tampão no lugar.
Passo 1
Primeiramente, temos que calcular a força exercida pela pressão interna. Sabemos que pressão é força sobre área, logo:
Repare que como a tensão está em Pa, devemos utilizar o diâmetro em metros.
Passo 2
Como temos a força atuante, devemos calcular a área de contato entre o tubo e o tampão:
Com a área e a força atuante, podemos calcular a tensão:
Resposta
Exercícios de Livros Relacionados
A lâmpada de engate do vagão ferroviário é sustentada pelo pino de 3m m de diâmetro em A . Se a lâmpada pesar 20N e o peso do braço extensor A B for 8N / m , determine a tensão de cisalhamento média n
Resolva o problema 1.61 para o pino B , qual está sujeito a cisalhamento duplo e tem 5 m m de diâmetro.
O alicate de pressão é usado para dobrar a extremidade do arame E . Se uma força de 100N for aplicada nas hastes do alicate, determine a tensão de cisalhamento média no pino emA . O pino está sujeito
A viga é apoiada por um pino em A e um elo curto B C . Determine o valor máximo P das cargas que a viga suportará se a tensão de cisalhamento média em cada pino não puder ultrapassar 80M P a . Todos o
O guindaste giratório está preso por um pino em A e suporta um montacargas de corrente que pode deslocar-se ao longo da flange inferior da viga, 0,3m ≤x ≤3,6m . Se a capacidade de carga nominal máxima