Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.6 - Ex. 108

O guindaste sobre esteiras equipado para demolição está se deslocando a uma velocidade constante de 3   k m / h quando é subitamente parado. Calcule o ângulo θ máximo por meio do qual o cabo da bola de demolição oscila.

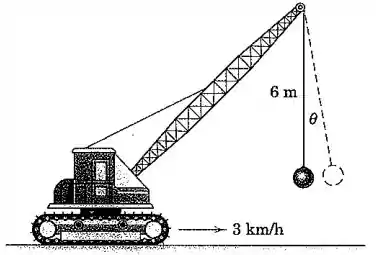
Passo 1

Inicialmente, o guindaste se locomove com uma velocidade v 0 = 3   k m / h = 0,833   m / s . Então, a bola também tem essa velocidade. Quando o guindaste para, a bola faz um movimento subindo até certa altura, fazendo um ângulo θ com a vertical, quando sua velocidade se anula, e ela retorna.

Essa mudança na altura da bola será:

h = L - L cos ⁡ θ = L 1 - cos ⁡ θ

onde L é a o comprimento do cabo.

Logo, a força peso realizará o seguinte trabalho sobre a bola:

U P = - m g h

U P = - m g L ( 1 - cos ⁡ θ )

Passo 2

Quando a bola atinge a altura h à sua posição inicial, a velocidade é nula. Então, a variação da energia cinética será:

Δ T = m v 2 2 - m v 0 2 2 = m 0 2 2 - m v 0 2 2

Δ T = - m v 0 2 2

Como a variação da energia cinética de um corpo é igual ao trabalho total realizado sobre ele, temos:

Δ T = U P

- m v 0 2 2 = - m g L 1 - cos ⁡ θ

v 0 2 = 2 g L - 2 g L cos ⁡ θ

cos ⁡ θ = 2 g L - v 0 2 2 g L

cos ⁡ θ = 1 - v 0 2 2 g L = 1 - 0,833 2 2 9,81 6

cos ⁡ θ = 0,994

θ = cos - 1 ⁡ 0,994

θ = 6,3 °

Resposta

θ = 6,3 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O anel de 2,5 kg é solto do repouso em A e desloca-se ao longo da guia sem atrito. Determine a velocidade do anel quando ele bate no apoio B. A mola tem um comprimento não deformado de 0,15m.
O anel de 2kg é submetido a uma velocidade para baixo de 4m/s quando está em A. Se a mola tem um comprimento não deformado de 1m e uma rigidez k=30N/m, determina a velocidade do anel em s=1m
O anel C de 4kg tem uma velocidade v A = 2 m/s quando está em A. Se a barra-guia é lisa, determine a velocidade do anel quando ele está em B. A mola tem um comprimento não deformado l a = 0,2 m.
O bloco de 375 N (massa =37,5 kg) é solto do repouso 1,5 m acima da placa. Determine a compressão de cada mola quando o bloco instantaneamente chega ao repouso após bater na placa. Despreze a massa da
Resolva o problema 14.18 utilizando a equação de conservação da energia