Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 44
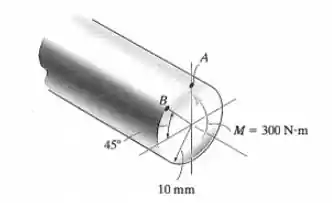
A haste de aço com diâmetro de está sujeita a um momento interno . Determine a tensão criada nos pontos e . Além disso, trace um rascunho de uma visão tridimensional da distribuição de tensão que age na seção transversal.
Passo 1
Show de bolinhas galerinha bonita, tudo beleza?
Saca só, nesse exercício aqui o enunciado nos diz que a haste de aço com diâmetro de está submetida a um momento interno de . Sabendo disso, ele nos pede para determinar a tensão criada nos pontos e .
Primeiramente, vamos precisar calcular o momento de inércia, que para seções circulares, é dado pela fórmula:
Também devemos calcular a distância da linha neutra, tanto de A, quanto de B. Esses dados serão necessários para calcular a tensão.
E para :
Passo 2
Como o momento é dado, podemos calcular as tensões em A e B pela fórmula:
Logo:
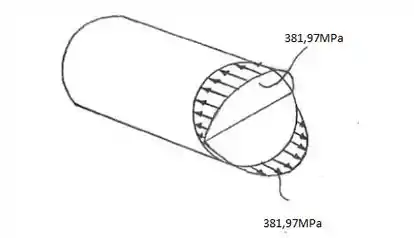
Representando o elemento, temos:
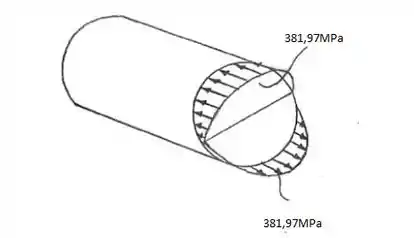
Resposta
