Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 63
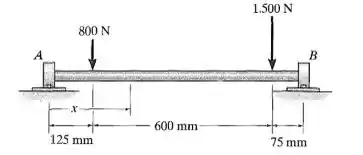
Se o eixo tiver um diâmetro de , determine a tensão de flexão máxima absoluta no eixo.
Passo 1
Primeiramente, devemos fazer o diagrama para determinarmos o maior momento atuante. Logo, vamos calcular as reações:
Com isso, podemos fazer o diagrama de cortante da estrutura:
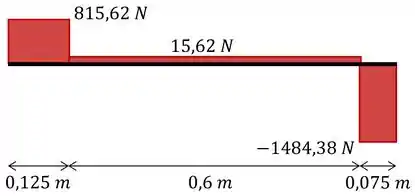
E o diagrama de momento fletor:
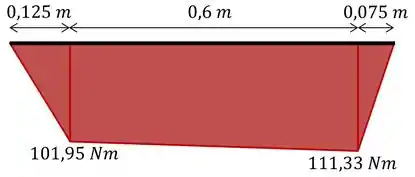
Passo 2
Com o momento máximo sendo 111Nm, podemos calcular a tensão máxima:
Resposta
Exercícios de Livros Relacionados
A viga é composta por quatro peças de madeira coladas como mostra a figura. Se o momento que age na seção transversal for M = 450N · m , determine a força resultante que a tensão de flexão produz na p
A peça de máquina feita de alumínio está sujeita a um momento M=75N m . Determine as tensões de flexão máximas tanto de tração quanto de compressão na peça.
A área da seção transversal da escora de alumínio tem forma de cruz. Se ela for submetida ao momento M=8k N . m , determine a tensão de flexão que age nos pontos A e B e mostre os resultados em elemen
Um eixo é feito de um polímero com seção transversal elíptica. Se ele resistir a um momento interno M=50 N . m , determine a tensão de flexão máxima desenvolvida no material (a) pela fórmula da flexão
A viga é composta por três tábuas de madeira pregadas como mostra a figura. Se o momento que age na seção transversal for M = 1,5k N . m , determine a tensão de flexão máxima na viga. Faça um rascunho