Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 112

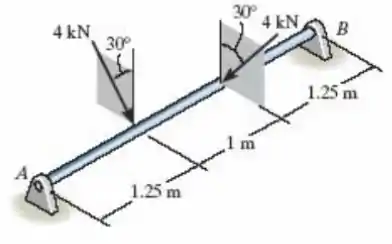
O eixo de aço de 65 mm de diâmetro está sujeito a duas cargas que agem nas direções mostradas na figura. Se os mancais em A e B não exercerem uma força axial sobre o eixo, determine a tensão de flexão máxima absoluta desenvolvida no eixo.

Passo 1

Faaaala, meu povo bonito!! Tudo bem com vocês?? Vamos continuar nossas questões sobre flexões. Nessa, ele nos diz que a barra está presa nos pontos A e B, que não fazem força no sentido do eixo dela (ou seja, só nos outros eixos – para cima e para o lado), e ainda tem duas forças sendo aplicadas com um ângulo de 30º com relação à normal. Depois de nos falar isso tudo, ele pede a tensão máxima absoluta sobre o eixo. Então, vamos lá!!

Passo 2

Primeira coisa que vamos fazer é o nosso DLC e decompor as forças sobre seus eixos.

Já sabemos que a soma dos momentos e das forças em torno de um eixo são zero. Então:

∑ M b   =   0

( 1,25 i ) ( - 3,464 j   –   2 k ) + ( 2,25 i ) ( - 3,464 j   +   2 k )   + ( 3,5 i ) ( A y j   -   A z k )   =   0

( 3,5 A z   –   2 ) j   +   ( 3,5 A y   –   12,124 ) k   =   0          

3,5 A z   –   2   =   0   ∴   A z   =   0,571   k N

3,5 A y   –   12,124   =   0   ∴   A y     =   3,464   k N

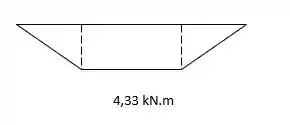
Agora que temos os valores das nossas reações de apoio, vamos montar nossos diagramas dos momentos nos eixos Y e Z.

Momento em Y:

Momento em Z:

Passo 3

Agora, meus querido xuxuzinhos, é só jogar naquela formulinha já manjada e partir pro abraço.

M m á x = M y 2   + M z ²   =   4,389   k N . m

σ m á x = M m á x   .   r I =   4,389   x   10 ³   x   0,0325 π 4 ( 0,0325 ) 4 = 163   M P a

Resposta

σ m á x = 163   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra prismática AB é construída de uma liga de bronze para a qual a curva de tensão-deformação específica em tração é mostrada na figura. Considerando que a curva de σ em função de ϵ é a mesma em
Um pequeno bloco de mateira suporta uma carga axial de 27 kN, como indicado. Determine a tensão no ponto A quando: (a) b = 0; (b) b = 38 mm; (c) b = 76 mm.
Uma barra prismática de seção transversal retangular é feita por uma liga para a qual a curva tensão-deformação específica pode ser representada pela relação ϵ = k σ 3 . Se um momento fletor M é aplic
Duas forças de 10 kN são aplicadas a uma barra retangular de 20 mm × 60 mm, como mostrado. Determinar a tensãono ponto A, quando: (a) b = 0; (b) b = 15 mm; (c) b = 25 mm.
Qualquer dar três cargas axiais, de intensidade P = 45 kN podem ser aplicadas na extremidade de um perfil de aço laminado w200 × 31,3. Determinar a tensão no ponto A: (a) para o carregamento mostrado;