Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 216
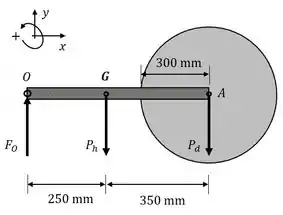
A haste e o disco circular articulado são liberados a partir do repouso na posição mostrada e oscilam no plano vertical em torno do mancal fixo em . A haste de tem um raio de giração em relação a de . O disco tem uma massa de . Supõe-se que os dois mancais estão sem atrito. Encontre a força exercida em sobre a haste imediatamente após a liberação e quando oscila através da posição vertical .
Passo 1
Uma haste está presa a um pino fixo em e a um disco em . O conjunto é solto quando a haste e o disco estão horizontais.
O peso da haste e o peso do disco irão girar o conjunto ao redor do pino em .
Queremos saber qual é a força no pino em duas situações:
- Caso : imediatamente após soltarmos o conjunto.
- Caso : quando o conjunto fica vertical, ao passar em .
Dados da questão:
- Massa da haste: .
- Raio de giração da haste em relação a :
- Distância do centro de massa da haste até : .
- Massa do disco: .
- Raio do disco:
- Distância do centro de massa do disco até :
Com calma, vamos ver um caso de cada vez! O plano é escrever as equações da dinâmica do problema e resolver para achar !
Passo 2
Primeiro o Caso . Vamos ver o diagrama de corpo livre.
Vamos usar o ponto como referencial e escrever as equações da dinâmica. Primeiro a versão linear:
Os sinais negativos são porque estamos supondo que as acelerações tangenciais da haste e do disco vão ser para baixo ! O conjunto vai girar no sentido horário!
As forças são simplesmente os pesos: , .
Mas aquelas acelerações ali são um problema... não fazemos ideia do valor delas. Vamos dar uma melhorada e pensar na aceleração angular ! Ela é a mesma para a haste e o disco (só o ângulo importa!), aí já fica mais fácil. Podemos passar da aceleração linear para angular multiplicando pela distância até o ponto !
Show, agora temos duas incógnitas. O que queremos descobrir e esse aí. Vamos ver como fica a dinâmica na versão angular, porque aí com certeza a aceleração angular vai aparecer lá.
Passo 3
Usando o ponto como referencial, a dinâmica angular nos diz que
Os sinais negativos são porque estamos supondo que a aceleração angular do conjunto vai ser no sentido anti-horário!
O momento de inércia da haste em relação a é fácil de calcular porque temos o raio de giração dele em relação a ! Podemos usar que
Quando ao disco, não tem momento no disco em relação ao centro dele . Então o disco não gira em relação ao ! Ele vai se mover ao redor do pino apenas! Aí é muuuuito fácil; o momento de inércia dele vai ser como se a massa estivesse concentrada em . Só usar a definição de momento de inércia:
De novo, as forças são simplesmente os pesos: , .
Sabemos todos esses caras menos o ! Então podemos calcular ele. Usando .
Ótimo! Agora é só voltar na versão linear:
Caso acabou! Vamos pro Caso .
Passo 4
O Caso vai ser quase a mesma coisa, mas temos uma diferença crucial: o conjunto agora em velocidade angular ao redor do ponto ! Não se confunda quanto a isso! O disco não está girando ao redor de !
Diagrama de corpo livre.
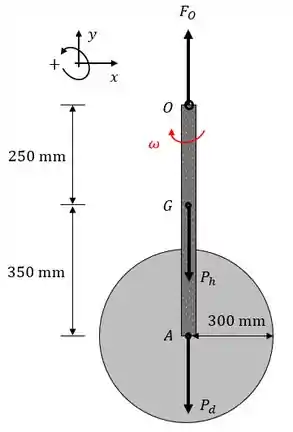
Vamos ver o que a dinâmica linear nos diz:
As acelerações aqui são centrípetas! O movimento no Caso está totalmente perpendicular à ação das forças. Então elas só estão atuando na mudança de direção! E como o centro de rotação está em , o sinal é positivo, porque as acelerações apontam para cima.
Podemos usar a fórmula para aceleração centrípeta, !
As forças são os pesos , , então temos duas incógnitas. O que queremos descobrir e essa velocidade angular aí. Dessa vez, a dinâmica angular não vai nos ajudar tão bem, porque nela aparece , não .
O jeito mais fácil para acharmos é olhando o balanço de energia!
Passo 5
A questão diz que não tem atrito. Então temos conservação de energia! Parte da energia potencial gravitacional que o conjunto tem no Caso vai virar energia cinética no Caso (a força da gravidade acelera o conjunto, fazendo trabalho).
Escrevendo isso pra fazermos conta, a variação da energia potencial gravitacional do conjunto, , vai ser a variação de energia cinética, .
Para o , só precisamos nos ligar na altura de cada parte do conjunto em relação a ! O centro de massa da haste varia uma altura . E o disco varia .
A variação de energia cinética é mais fácil ainda! Todo mundo estava parado quando o conjunto estava horizontal. E agora todo mundo está com velocidade ! Aproveita que já deduzimos os momentos de inércia no Passo .
Agora só substituir em !
Nem precisa fazer a raiz quadrada! É esse cara mesmo que a gente quer!
Use em :
Resposta
Força em imediatamente após a liberação do conjunto:
Força em quando o conjunto passa pela posição vertical: