Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.3 - Ex. 68
Desenvolva uma expressão para a transmissibilidade para o sistema da figura. Essa relação é definida como a força máxima transmitida à base dividida pela amplitude da função de forçamento. Expresse sua resposta em termos de e do fator de amplificação .
Passo 1
Dados da questão:
- Massa: .
- Rigidez da mola:
- Coeficiente de amortecimento:
- Forçamento:
Uma massa recebe um forçamento sobre ela. A base resiste com forças e relacionadas a suas propriedades elásticas e de amortecimento.
Queremos descobrir a razão entre a força máxima na base e a amplitude de .
Passo 2
Primeiro, vamos achar a equação do movimento.
Escolha uma posição de referência e aí tome um deslocamento qualquer. Vamos usar como referência a posição de equilíbrio e considerar o movimento para baixo como positivo!
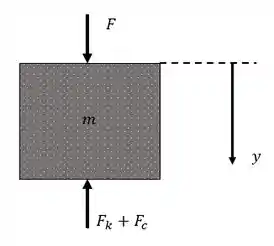
Como estamos usando a posição de equilíbrio, não precisa se preocupar com peso nem nada disso porque a mola já da conta do recado, equilibrando.
A dinâmica fica:
A mola gera uma força elástica e a o amortecedor resiste à variação de velocidade com . Substituindo isso e
Ótimo! Temos a equação do movimento e ela está na forma mais simples. Podemos dividir pela massa e aí usar a frequência natural e o fator de amortecimento :
Agora que sabemos do que estamos tratando, vamos achar o que a questão pede!
Passo 3
Para calcular o tal , precisamos saber a força máxima exercida sobre a base. A força transmitida para a base em algum instante de tempo é
Como nossa equação do movimento está na forma usual dela, sabemos que a deslocamento em regime permanente toma forma
Estamos olhando somente o permanente porque é geralmente o que interessa para esse conceito aí de transmissibilidade. Tá, continuando:
Queremos o valor máximo desse cara! Aqui tem um truque bem legal. Quando tiver senos e cossenos com mesmo argumento (mesmo carinha dentro do parênteses), você pode assumir que de algum jeito dá pra escrever assim:
E pra que fazer isso? Porque é fácil ver quem é o valor máximo de ! É !!
Vamos achar !
Passo 4
Expanda com fórmula pra soma de arcos:
Compare com a expressão original que você tem: . Pra essa maluquice funcionar (ser igual), é preciso que
Agora eleva tudo ao quadrado e soma!
Ótimo! Agora vamos só dar uma ajeitada. A questão pede o resultado segundo e o fator de amplificação .
Esse fator é a razão entre (amplitude do deslocamento) e (amplitude em um deslocamento com forçamento fixo .
Vamos usar também e :
E como
FINALMENTE a gente calcula o que a questão quer:
Resposta
Transmissibilidade: