Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas fundamentais - Ex. 24
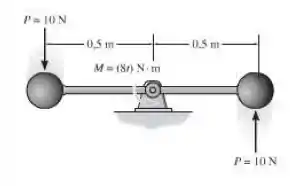
Duas esferas idênticas de estão fixadas em uma barra leve e rígida, a qual gira no plano horizontal centrada em . Se aas esferas estão sujeitas a forças tangenciais , e a barra está sujeita a um momento de binário , onde está em segundos, determine a velocidade das esferas no instante . O sistema parte do repouso. Despreze a dimensão das esferas.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
A partir do conceito de conservação da quantidade de movimento angular e impulso, temos:
Resposta
Exercícios de Livros Relacionados
Resolva o Problema 19.168, supondo que um dashpot de constante c = 6500 N⋅s / m seja introduzido entre o motor e o solo.19.168 - Um motor de 400 kg apoiado por quatro molas, cada uma com 150 kN / m co
Um motor de 400 kg apoiado por quatro molas, cada uma com 150 kN / m constantes, é obrigado a se mover verticalmente. Sabendo que o desequilíbrio do rotor é equivalente a uma massa de 23 g localizada
Uma placa quadrada fina do lado a pode oscilar em torno de um eixo AB localizado a uma distância b de seu centro de massa G. (a) Determine o período de pequenas oscilações se if b = 1 2 a ⋅ ( b ) Dete
Duas hastes, cada uma com massa m e comprimento L, são soldadas para formar o conjunto mostrado. Determine (a) a distância b para a qual a frequência de pequenas oscilações da montagem é máxima, (b) a
19.114. À medida que a velocidade de rotação de um motor de 100 kg apoiado por molas é aumentada, a amplitude da vibração, causada pelo desbalanceamento do seu rotor de 15 kg, primeiro aumenta e depoi