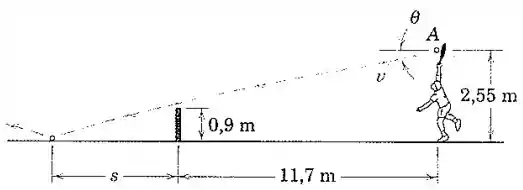
Se o jogador de tênis dá o saque horizontalmente , calcule sua velocidade se o centro da bola transpõe a rede de por . Encontre também a distância a partir da rede até o ponto onde a bola atinge a superfície da quadra. Despreze a resistência do ar e do efeito da rotação da bola.

Galera, para que a bola transponha a rede de por , precisamos que, quando , tenhamos , considerando o pé do jogador como a origem do sistema de coordenadas e o eixo positivo para a esquerda. Então, se tivermos a equação da trajetória parabólica que a bola faz, ou seja, se encontrarmos uma equação que nos dê em função de , poderemos encontrar a velocidade .

Pra obtermos isso, começamos equacionando o movimento horizontal:

Para o movimento vertical, teremos:

Substituiremos a expressão de encontrada:

Aí temos a nossa equação da trajetória!