Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 105
Um homem de tenta baixar a caixa de usando uma corda que passa por um pino rugoso. Determine o menor número de voltas além da volta básica ( em torno do pino para realizar o trabalho. Os coeficientes de atrito estático entre a corda e o pino e entre os sapatos do homem e o solo são e , respectivamente.
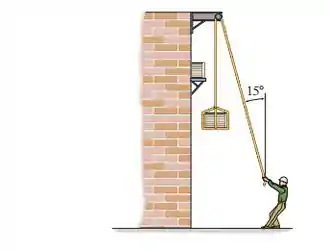
Passo 1
Primeiro vamos analisar o homem, se liga nessa ilustração:
Como o homem está em equilíbrio, em temos:
Assim,
No eixo
Como :
Passo 2
Agora vamos resolver aquele sistema!
Assim,
e
Agora vamos fazer aquela brincadeira com o atrito na roldana! A expressão é a seguinte:
Como é a força no sentido do movimento, . E portanto,
Passo 3
Agora vamos arrumar as coisas pra não ficar confuso.
Substituindo os valores conhecidos:
Logo,
O nosso ângulo será , pois temos a volta básica mais voltas.
Fazendo as contas:
Então o número de voltas necessárias são duas.