Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 6.Problemas - Ex. 98
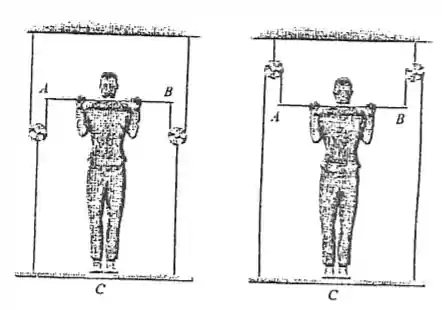
Um homem com peso de tenta se suspender usando um dos dois métodos mostrados. Determine a força total que ele precisa exercer na barra em cada caso e a reação normal que ele exerce na plataforma em . Despreze o peso da plataforma.
Passo 1
Como o enunciado foi bem direto com relação ao que ele deseja vamos avaliar o problema para o primeiro caso ao qual chamaremos de e para o segundo caso que chamaremos de . Dessa forma, tomemos os seguintes diagramas de forças
Passo 2
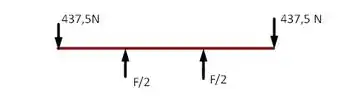
Para o caso vamos ter para a barra
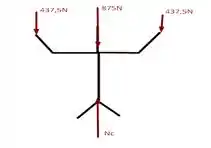
Para o homem
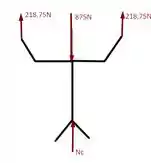
Já para o caso teremos para a barra
E para o homem
Resposta
Exercícios de Livros Relacionados
3.21. Se a tração desenvolvida em cada um dos quatro fios não pode exceder 600N , determine a maior massa do candelabro que pode ser suportada.
3.25. Determine o peso máximo do balde que o sistema de fios pode suportar, de modo que nenhum fio desenvolva uma tração maior que 0,5k N .
Desenhe o diagrama de corpo livre do membro AB , que esta apoiado por um rolete em A e por um pino em B. Explique o significado de cada força em ação no diagrama
Desenhe o diagrama de corpo livre da barra , que possui uma espessura desprezível e pontos de contatos lisos em A, B e C. . Explique o significado de cada força em ação no diagrama
Desenhe o diagrama de corpo livre do membro ABC , que esta sustentado que é sustentado por um anel liso em A, um rolete em B e uma ligação curta em CD . Explique o significado de cada força em ação no