Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 11.Problemas fundamentais - Ex. 1
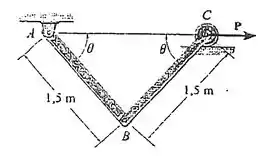
Determine a intensidade exigida da força para manter o equilíbrio do mecanismo em . Cada membro tem uma massa de kg.
Passo 1
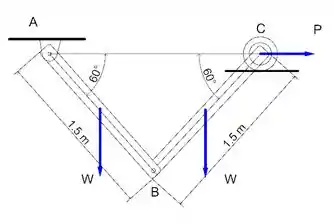
Vamos começar fazendo um diagrama de forças ativas, as forças que podem vir a gerar um trabalho virtual:
Passo 2
Sabemos pelo Princípio do Trabalho Virtual que o somatório do trabalho das nossas forças ativas é nulo:
O deslocamento que o trabalho virtual do peso de cada barra causaria é:
Enquanto que o deslocamento causado pela força é:
Passo 3
Agora precisamos derivar isso em função de , ficamos com:
E para a segunda equação:
Passo 4
Podemos então substituir nossas informações no somatório do trabalho virtual:
Como
Utilizando o ângulo fornecido e o peso dada a massa , chegamos em:
Resposta
Exercícios de Livros Relacionados
13. Determine os ângulos θ para equilíbrio do disco de 20N ( ≈ 2k g ) usando o princípio do trabalho virtual. Despreze o peso da barra. A mola está livre quando θ = 0 ° e sempre permanece na vertical
14. O caminhão é pesado na balança de inspeção da rodovia. Se uma massa conhecida m é colocada a uma distância s do fulcro B na balança, determine a massa do caminhão m t se seu centro de gravidade es
20. A máquina mostrada é usada para dar forma a chapas de metal. Ela consiste em duas articulações A B C e D E F , que são operadas pelo cilindro hidráulico. As articulações empurram a barra móvel G p
11. Se a mola tem uma rigidez k e um comprimento livre l 0 determine a força P quando o mecanismo está na posição mostrada. Despreze o peso dos membros.
19. A mola está livre quando θ = 45 ° e tem uma rigidez k = 20k N / m . Determine o ângulo θ para equilíbrio se cada um dos cilindros pesa 250N . Despreze o peso dos membros. A mola permanece horizont