Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 21
3.21. Se a tração desenvolvida em cada um dos quatro fios não pode exceder , determine a maior massa do candelabro que pode ser suportada.
Passo 1
Falaaa! Queremos a maior massa que o candelabro pode ter, sabendo que a maior força nesses fios não pode ultrapassar 600 N.
Primeira coisa a fazer nesse tipo de exercício é o diagrama de corpo livre. Vamos fazer para os pontos e :
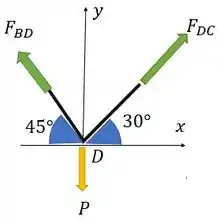
Para resolver esse exercício usaremos as equações de equilíbrio nos eixos x e y. Primeiro faremos isso para o ponto D da figura, onde estarão agindo e o peso do candelabro.
Depois disso faremos a mesma coisa para o ponto B na figura.
Dessa forma, descobriremos quem é a maior força atuando nos cabos e quem é máxima. Vamos!
Passo 2
Como estamos no equilíbrio, as forças resultantes nos eixos precisam zerar
Aí a gente acha expressões para essas forças e iguala a zero.
Vamos começar calculando no ponto D.
Então
Agora vamos fazer o mesmo para
Passo 3
Agora temos duas incógnitas (sem contar com ) e duas equações, vamos resolva-las.
Aqui a gente pode usar um truque, repare que , então se somarmos as equações teremos
Considerando
Conseguimos em função de . Vamos achar uma expressão assim para todas as forças.
Passo 4
Agora com podemos determina
Passo 5
Agora vamos usar a equação de equilíbrio no ponto B. Novamente as resultantes zera.
Então
Agora o eixo x
Vamos isolar
Passo 6
Note que é maior do que todas as outras forças, então se for menor que todas as outras forças também serão consequentemente, logo