Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 187

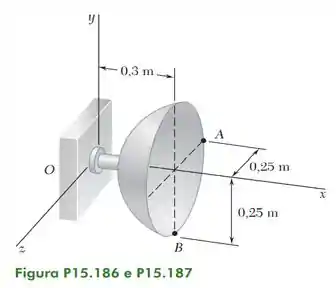
No instante considerado, a antena de radar mostrada na figura gira em torno da origem das coordenadas com uma velocidade angular ω = ω x i ^ + ω y j ^ + ω z k ^ . Sabendo que v A x =   10 0   m m / s , v A y =   - 9 0   m m / s e v B z =   12 0   m m / s , determine (a) a velocidade angular da antena, (b) a velocidade do ponto A

Passo 1

Bora pra questão 184 agora, meus caros (as)!

Bom! Temos que determinar a aceleração angular do conjunto de pás, sabendo que, no instante mostrado na figura, a velocidade angular e a aceleração angular da caixa do motor são...

ω 2 = - 2,5   r p m i ^

α 2 = 0 .

Pois muito bem! Antes de qualquer coisa, vamos a algumas convenções...

Primeiro o sentido de rotação... Normalmente costumamos chamar o sentido horário de negativo e o sentido anti-horário de positivo.

Sendo assim, vamos reescrever ω 1 e ω 2 ... Dessa vez, passando pra r a d / s :

ω 1 = - 360   r p m i ^

ω 1 = - 360 ⋅ 2 π 60 r a d s i ^

ω 1 = - 12 π   r a d / s i ^

ω 2 = - 2,5   r p m j ^

ω 2 = - 2,5 ⋅ 2 π 60 r a d s j ^

ω 2 = - 0,08333 π   r a d / s j ^

Passo 2

Pronto! As informações mais importantes, já temos em mãos!

Agora se liga! Primeiro precisamos determinar a taxa de rotação com que o plano O x y z está girando, ou seja, a velocidade angular!

Pois muito bem! Essa taxa é a velocidade angular da caixa do motor, pois é ela que faz todo o sistema funcionar. Sendo assim;

Ω = ω 2

Ω = - 0,08333 π   r a d / s j ^

Assim, a aceleração angular será dada por...

α = ω ˙ 1 + ω ˙ 2

α = ω ˙ 1 + ω ˙ 2 O x y z + Ω × ( ω 1 + ω 2 )

α = 0 + 0 + [ - 0,08333 π   r a d / s j ^ ] × ( - 12 π i ^ - 0,08333 π j ^ )

α = - π 2 k ^

α ≅ - ( 9,87   r a d / s 2 )   k ^

Pronto! Finalizamos aqui! Até a próxima!

Resposta

α ≅ - ( 9,87   r a d / s 2 )   k ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

28. . Por um certo período, a engrenagem A do motor de arranque do autmovel gira com uma aceleração angular a A = 50 ω 0,5r a d / s 2 , onde w é dado em rad/s. Determine a velocidade angular e o deslo
27. Por um certo período, a engrenagem A do motor de arranque do autmovel gira com uma aceleração angular a A = 450 t 2 + 60r a d / s 2 , onde t é dado em segundos. Determine a velocidade angular e o
39. Determine a velocidade e a aceleração da plataforma P como uma função do ângulo θ do came C se o came gira com uma velocidade angular constante ω . O pino de conexão não interfere no movimento de
46. No instante que θ=30°, a manivela AB gira com uma velocidade angular e aceleração angular de ω=10rads e α=2rads2, respectivamente. Determine a velocidade e aceleração do bloco deslizante C nesse i
38. O bloco se descola para a esquerda com uma velocidade constante v 0 . Determine a velocidade angular e aceleração angular da barra como uma função de θ .