Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 115

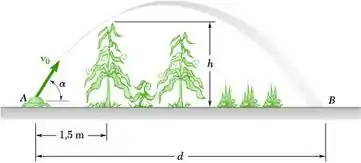
Um irrigador oscilante de jardim, que lança um jato de água com uma velocidade inicial v0 de 8 m/s, é usado para irrigar uma horta. Determine a distância d para o ponto mais afastado B que será irrigado e o ângulo α correspondente quando (a) os vegetais estiverem apenas começando a crescer e (b) a altura h de um pé de milho for de 1,8 m.

Passo 1

Fala ai pessoal tudo beleza? O enunciado pede que a gente determine distância d para o ponto mais afastado B que será irrigado e o ângulo α correspondente quando (a) os vegetais estiverem apenas começando a crescer e (b) a altura h de um pé de milho for de 1,8 m.

v x 0 = v 0 cos ⁡ α = 8   m/s cos ⁡ α

v y 0 = v 0 sin ⁡ α = 8   m/s sin ⁡ α

Movimento horizontal. (Uniforme)

x = 0 + v x 0 t = 8 cos ⁡ α t

No Ponto B:

x = d :             d = 8 cos ⁡ α t

t B = d 8 cos ⁡ α

Passo 2

Movimento vertical. (Movimento uniformemente acelerado)

y = 0 + v y 0 t - 1 2 g t 2

= 8 sin ⁡ α t - 1 2 g t 2               g = 9.81   m/ s 2

Passo 3

No Ponto B:

0 = 8 sin ⁡ α t B - 1 2 g t B 2

Simplificando e substituindo por tB

0 = 8 sin ⁡ α - 1 2 g d 8 cos ⁡ α

d = 64 g sin ⁡ 2 α

Passo 4

  1. Quando h = 0, a água pode seguir qualquer trajetória fisicamente possível. Em seguida, segue da Eq. (1) que d é máximo quando 2 α = 90 °

    2. Então

    d = 64 9.81 sin ⁡ 2 × 45 °

    Passo 5

  2. Baseie-se na Eq. (1) e os resultados da Parte a, pode-se concluir que d aumenta de valor à medida que α aumenta de valor de 0 para 45 ° e d diminui à medida que ir aumenta ainda mais. Assim, dmax ocorre para o valor de α mais próximo de 45 ° e para o qual a água passa apenas pela primeira linha de plantas de milho. Nesta linha, xcom = 1.5 m

de modo a

t milho = 1.5 8 cos ⁡ α

Também com ymilho = h, temos

h = 8 sin ⁡ α t milho - 1 2 g t milho 2

Substituindo tmilho e notando h = 1,8 m

1.8 = 8 sin ⁡ α 1.5 8 cos ⁡ α - 1 2 g 1.5 8 cos ⁡ α 2

1.8 = 1.5 tan ⁡ α - 2.25   g 128   cos 2   α

1 cos 2   α = sec 2   α = 1 + tan 2   α

1.8 = 1.5 tan ⁡ α - 2.25 9.81 128 1 + tan 2   α

ou

0.172441   tan 2   α - 1.5 tan ⁡ α + 1.972441 = 0

Resolvendo

α = 58.229 °             e             α = 81.965 °

Finalmente, usando a Eq. (1)

d = 64 9.81 sin ⁡ 2 × 58.229 °

Resposta

a )   α = 45 °

d max = 6.52   m

b )   Da discussão acima, segue-se que   d = d max   quando

α = 58.2 °

d max = 5.84   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

À medida que foi observado um navio se movendo para o leste a 9 km/h, o vento parecia soprar do sul. Depois que o navio mudou de curso e velocidade, e este se movia para o norte a 6 km/h, o vento pare
Determinar a velocidade periférica de uma cabine de teste de centrifugação para que a componente normal da aceleração seja 10g.
Em um teste de desempenho, dirige-se um automóvel ao longo de uma pista de teste circular de diâmetro d. Determine (a) o valor de d quando a velocidade do automóvel é 72 km/h e a componente normal da
Determine a velocidade escalar máxima que os carros da montanha-russa podem atingir ao longo da seção circular AB da pista se o componente normal de sua aceleração não pode exceder 3g.
Um jogador de golfe lança uma bola a partir do ponto A com uma velocidade inicial de 50 m/s e um ângulo de 25° com a horizontal. Determine o raio de curvatura da trajetória descrita pela bola (a) no p