Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 63
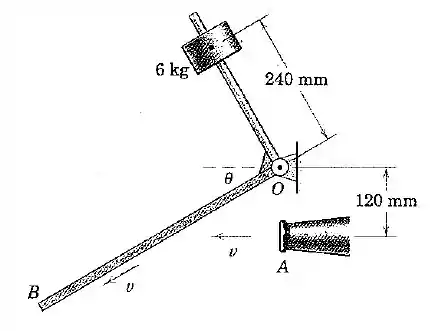
Um jato de ar em alta velocidade escoa do bocal com de diâmetro a uma velocidade de e atinge a pá , mostrada em sua vista lateral. A pá e sua extensão em ângulo reto têm massas desprezíveis comparadas com o cilindro preso de e são livremente articuladas em torno de um eixo horizontal através de . Calcule o ângulo assumido pela pá com a horizontal. A massa específica do ar nas condições presentes é . Declare quaisquer hipóeses utilizadas.
Passo 1
Vamos começar calculando a taxa de escoamento de massa do jato de ar:
E agora podemos calcular a força resultante sobre esse jato:
Dessa vez o módulo da variação de velocidade é um pouco mais complicado de calcular, porque os dois vetores (final e inicial) não são paralelos.
Vamos fazer um desenho ilustrando a situação:
A variação que estamos procurando é o módulo do vetor preto . Como o módulo de todos esses vetores é igual a , ficamos com a seguinte expressão:
E então:
Passo 2
Agora, como estamos interessados no ângulo , precisamos pensar em termos de torque.
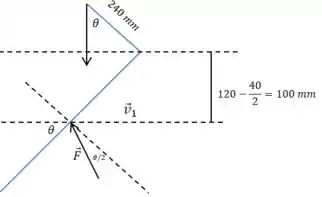
O torque gerado pela força que acabamos de calcular, e que age na direção de , é:
E o torque gerado pelo peso do cilindro de :
E o sinal negativo aparece porque o peso do cilindro favorece a rotação no sentido oposto ao do jato de ar.
Passo 3
Quando o sistema estiver em equilíbrio, vamos ter a seguinte igualdade:
Usando o fato de que:
Então:
E a única hipótese “não-usual” que utilizamos nessa conta foi a ideia de que o jato de ar se comporta exatamente como no nosso desenho, sem ser espalhado para outras direções.
Resposta
A pá assume um ângulo de com a horizontal.