Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 64
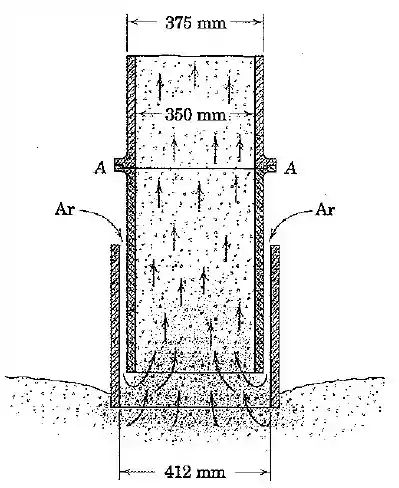
Um corte axial do bocal de sucção para um descarregador de trigo a granel é mostrado aqui. O tubo externo é preso ao tubo interno por várias nervuras longitudinais que não limitam o escoamento do ar. Um vácuo de de mercúrio ( manométrica) é mantido no tubo interno, e a pressão através do fundo do tubo externo é a atomsférica (). O ar a é aspirado através do espaço entre os tubos a uma taxa de à pressão atmosférica e aspira consigo de trigo por hora para cima no tubo a uma velocidade de . Se a unidade do bocal abaixo da seção - tem uma massa de , calcule a compressão na conexão em -.
Passo 1
Vamos começar calculando a área pela qual o ar entra no sistema:
E agora a área do tubo interno é:
O enunciado ainda diz que o ar é aspirado pelo tubo a uma taxa de , ou seja:
E o trigo escoa a uma taxa de , ou seja:
Com esses dados já podemos calcular a velocidade pela qual o ar entra no sistema:
Passo 2
Ok, agora já temos as informações básicas do sistema. Nosso objetivo é calcular a compressão na conexão .
Essa compressão é uma das forças que mantém o escoamento no sistema, então vamos escrever a equação da força resultante:
Começando pelo termo da direita, temos que somar separadamente os produtos relativos ao trigo e ao ar:
E o foi dado no enunciado, é a velocidade com que a mistura sobe o tubo interno.
Passo 3
Beleza, vamos olhar para o trecho em que está a conexão . Estamos olhando para um fluido subindo pelo tubo, e já vimos que ele precisa estar sujeito a uma força resultante de . No trecho em questão, as forças sobre a mistura são:
Onde é a força realizada pela pressão de vácuo no tubo interno, é o peso da unidade abaixo da seção que estamos calculando e é a força que a conexão imprime sobre a mistura:
Agora vamos resolver essa equação:
Resposta
A compressão é de .