Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 60
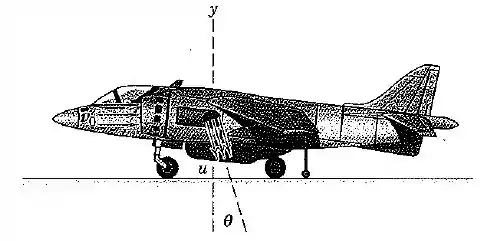
A aeronave militar (decolagem e aterrisagem vertical na sigla em inglês) é capaz de subir verticalmente sob a ação da descarga de seu jato, que pode ser direcionada desde para decolar e pairar até para voar em frente. A aeronave carregada possui uma massa de . Na potência plena de decolagem, o seu motor turbo-fan consome ar na taxa de e tem uma razão ar/combustível de . A velocidade de exaustão dos gases é essencialmente na pressão atmosférica através dos bocais de saída. O ar com uma massa específica de é sugado para as aberturass de admissão na pressão de (manométrica) sobre a área total de admissão de . Determine o ângulo para decolagem vertical e a correspondente aceleração vertical da aeronave.
Passo 1
Bom, se o avião quer decolar perfeitamente na vertical, ele precisa anular completamente as forças na direção horizontal. É isso que vai definir o ângulo que queremos calcular.
Vamos começar calculando a força produzida pelo escoamento do ar. A taxa de escoamento de massa nas aberturas de admissão (onde só temos ar) é:
E a velocidade desse fluxo de admissão pode ser calculanda usando a fórmula:
Isso quer dizer que a “força de entrada” é:
A taxa de escoamento de massa na saída (onde temos ar e combustível) é:
Já que a razão ar/combustível é , segundo o enunciado. E a velocidade nesse duto de saída é , então a “força de saída” é:
Passo 2
Agora vamos voltar a pensar na força resultante na direção :
Além da resultante das forças de escoamento que acabamos de calcular, também precisamos considerar o efeito da pressão sobre a área das aberturas de admissão.
Não podemos esquecer de projetar tudo no eixo horizontal. A força associada à pressão e a força de entrada já estão paralelas a , mas a força de saída forma um ângulo de acordo com a figura.
Passo 3
E agora para calcular a aceleração vertical é só usar a segunda lei de Newton:
Na vertical temos apenas a outra componente da força de saída competindo com o peso do avião:
Resposta
O ângulo para decolagem vertical é e a aceleração vertical correspondente é .