Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.5 - Ex. 100
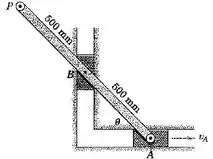
5/100) O movimento da barra é controlado pelas trajetórias restritas de e . Se a velocidade angular da barra é de no sentido anti-horátioquando a posição é ultrapassada , determine as velocidades dos pontos e .
Passo 1
Bom pessoal , seja o ponto de encontro das retas perpendiculares às velocidades dos pontos indicados na barra . Sendo assim , temos que :
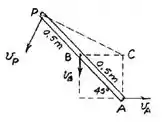
Aplicando Pitágoras , obtemos que :
Passo 2
Então galera , agora fica tudo mais fácil . Utilizando a relaão aprendida nesta seção , achamos que :
Da mesma forma , temos que :
Logo ,
Resposta
Exercícios de Livros Relacionados
Um pequeno colar pesando 2 lb é rigidamente preso a uma haste uniforme de 6 lb de comprimento. L = 3 pés. Determine (a) a distância d para maximizar a frequência de oscilação quando a barra recebe um
Para a placa triangular equilateral uniforme de lado l = 300 mm, determine o período de pequenas oscilações se a placa estiver suspensa em (a) um de seus vértices e (b) no ponto médio de um de seus la
Uma plataforma horizontal P é mantida por várias barras rígidas que são conectadas a um fio vertical. O período de oscilação da plataforma é de 2,2 s quando a plataforma está vazia e 3,8 s quando um o
Uma placa retangular delgada de lados aeb é suspensa por quatro fios verticais do mesmo comprimento l. Determine o período de pequenas oscilações da placa quando (a) ela é girada em um pequeno ângulo
Uma haste delgada AB de comprimento / = 600 mm e massa desprezível é conectada a dois colares, cada um com 8 kg de massa. O colar A está preso a uma mola de constante k = 1.2 kN/m e. pode deslizar em