Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 17
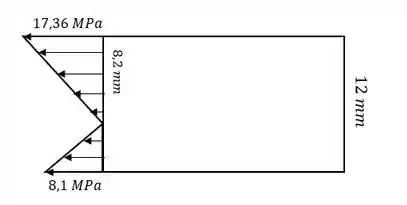
A junta está sujeita a uma força de , como mostra a figura. Faça um rascunho da distribuição da tensão normal que age na seção se a seção transversal retangular do elemento tiver largura de e espessura de .
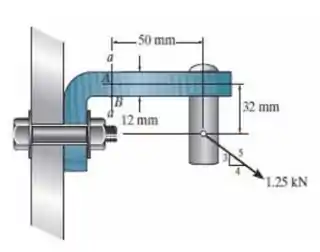
Passo 1
Fala aí galera, bora garantir aquele notão em Resmat? Para isso temos que resolver mais questões. Primeiro, vamos fazer o DCL:
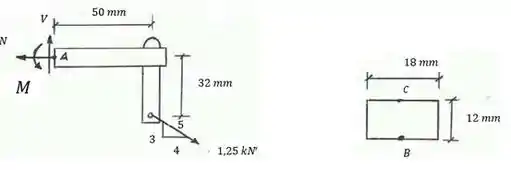
Passo 2
Com isso, podemos calcular o momento e o equilíbrio. Para o equilíbrio, temos:
E para o momento, temos:
Passo 3
Em seguida, devemos calcular a tensão de tração máxima , temos:
Agora, vamos calcular a tensão de compressão máxima, temos:
Passo 4
Por fim, precisamos estabelecer corte. Para isso, vamos usar a semelhança de triângulos. Fica assim:
Com isso, nosso esboço vai ser:
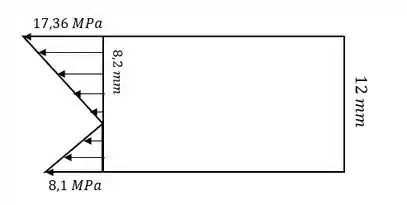
Resposta
Exercícios de Livros Relacionados
O pino de suporte sustenta a carga de 3,5 kN. Determine as componentes da tensão no elemento estrutural do suporte no ponto B. O suporte tem 12 mm de espessura.
A viga suporta a carga mostrada na figura. Determine o estado de tensão nos pontos E e F na seção a-a e represente os resultados em um elemento de volume diferencial localizado em cada um desses ponto
A viga em balanço é usada para suportar a carga de 8 kN. Determine o estado de tensão nos pontos A e B e trace um rascunho dos resultados sobre os elementos diferenciais localizados em cada um desses
O painel de sinalização uniforme pesa 7,5 kN e é suportado pelo tubo AB que tem raio interno de 68 mm e raio externo de 75 mm. Se a parte frontal do painel estiver sujeita a uma pressão uniforme do ve
O eixo de 18 mm de diâmetro é submetido à carga mostrada na figura. Determine as componentes da tensão no ponto A. Trace um rascunho dos resultados em um elemento de volume localizado nesse ponto. O m