Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 31
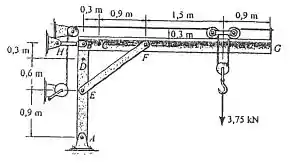
A lança do guindaste suporta uma carga de através do carrinho que desliza por cima da lança. Determine a força normal interna, o esforço cortante e o momento no ponto da lança quando o carrinho está na posição mostrada. Os membros do guindaste estão interligados por um pino em , e e por uma ligação curta .
Passo 1
Para determinar o que se pede, deve-se fazer o diagrama de corpo livre dos membros da viga para que seja possível determinar alguma reação agindo nela. Após isso, deve-se seccionar o corpo nos pontos de referência e fazer a análise dessas seções, ou seja, fazer a análise das reações internas de cada membro seccionado.
Para este caso pode-se fazer a análise do segmento a fim de determinar a força exercida pela conexão para encontrar as reações em A e, então, determinar as reações internas em .
Passo 2
Para iniciar, podemos realizar a análise do membro que terá o DCL dado por:
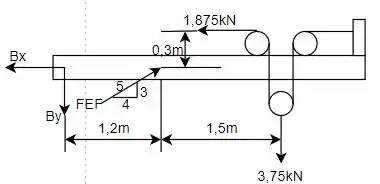
Então, para determinar as reações agindo na viga deve-se primeiro encontrar o valor da força . Isso pode ser feito através do princípio dos momentos em relação ao ponto . Então, considerando o sentido anti-horário como positivo:
Passo 3
Com o valor de definido, se torna possível descobrir o valor de suas componentes e, também, fazer as equações de equilíbrio para os dois eixos coordenados.
Dessa forma, passando agora a análise para o guindaste inteiro, o DCL será:
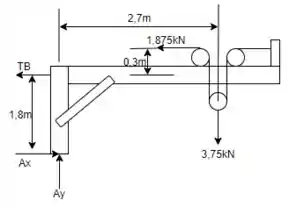
Sendo assim, tendo o sentido anti-horário como positivo e fazer o somatório de momentos em realação ao ponto , tem-se:
Além disso, para o eixo :
E para o eixo :
Passo 4
Por fim, para determinar as reações internas no ponto , deve-se fazer um “corte” neste ponto e aplicar as equações de equilíbrio. O DCL desta seção será:
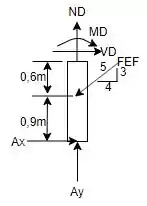
Assim, teremos para o eixo :
Em seguida, para o eixo :
E, considerando o sentido anti-horário como positivo para fazer o somatório de momentos em relação ao ponto :