Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 117
Uma corda uniforme é suspensa entre dois pontos com a mesma elevação. Determine a razão entre a flecha e o vão, de modo que a tração máxima na corda seja igual ao peso total da corda.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Aqui temos uma corda com carregamento uniforme suspensa entre dois pontos. O nosso objetivo é determinar a razão entre a flecha (altura ) e o vão (comprimento ), como podemos ver no esboço abaixo:
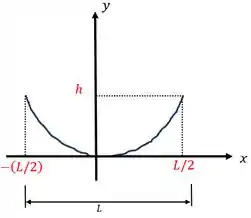
Como esta é uma corda que cujas equações foram desenvolvidas nos exercícios anteriores (inclusive até no Exemplo 7.13), então, vamos utilizar diretamente as equações.
Então, vamos para as contas!
Passo 2
O nosso objetivo é determinar a razão flecha e o vão . Então, para que a gente calcule a altura da flecha, temos a seguinte equação:
Mas que a gente não sabe nada ainda.
Continuando, a questão também nos diz que a razão é tal que a tração máxima no cabo é igual ao peso! Opa, temos uma informação muito importante aqui!
Relembrando, a tração máxima é dada por:
Este ângulo ocorre no ângulo de maior inclinação (maior valor ), e que neste caso ocorre nas extremidades, em . Como , temos:
Ao utilizarmos relações trigonométricas conseguimos passar de para , como vemos abaixo:
Continuando, como a tração deve ser igual ao peso, temos:
E assim a gente para de trabalhar com a restrição da tração!
Passo 3
Agora que a gente terminou a parte da tração igual ao peso e conseguimos obter quem é , basta trabalharmos com a equação da flecha!
Como queremos descobrir a altura , basta substituir na equação da flecha e verificar o valor final. Portanto,
OBS: Como , então
E assim finalizamos a questão!