Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 24

A largura das abas da viga é b = 200   m m . Se a tensão de flexão máxima não puder ultrapassar σ a d m = 160   M P a , determine o maior peso da máquina que a viga pode suportar. O centro de gravidade da máquina se encontra em G e os apoios em B e C são lisos.

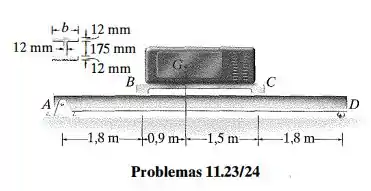
Passo 1

Dados da questão: b = 200   m m ,   σ a d m = 160   M P a ,   t = 12 m m ,   h = 175   m m ,   L 1 = 1,8   m ,   L 2 = 0,9   m ,   L 3 = 1,5   m ,   L 4 = 1,8   m

A questão pede o peso máximo da carga W = ?

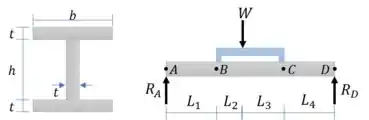
Passo 2

Vamos começar calculando as forças que atuam nos pontos B e C

∑ M C = 0 ⇒ F B ⋅ ( L 2 + L 3 ) - W ⋅ L 3 = 0

F B = 1,5 2,4 W

F B = 0,625 W

∑ F Y = 0 ⇒ F B - W + F C = 0

F B = W - F C

F B = 0,375 W

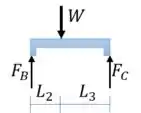
Passo 3

Agora vamos calcular as reações de apoio:

∑ M D = 0 ⇒ R A ⋅ L 1 + L 2 + L 3 + L 4 - 0,625 W ⋅ L 2 + L 3 + L 4 - 0,375 W ⋅ L 4 = 0

6 ⋅ R A - 0,625 W ⋅ 4,2 - 0,375 W ⋅ 1,8

R A = 0,55 W

∑ F Y = 0 ⇒ R A - 0,625 W - 0,375 W + R D = 0

R D = 0,45 W

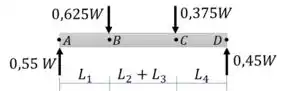
Passo 4

Vamos utilizar a Tabela 6.1 para gerar diagramas de esforço cortante e momento fletor pelo método gráfico.

V m a x = 0,55 ⋅ W

M m a x = 0,55 ⋅ L 1 ⋅ W

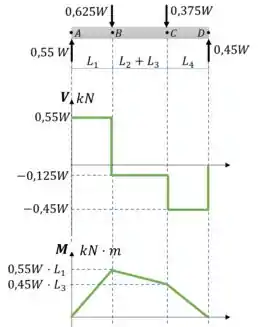
Passo 5

Vamos calcular o momento de inércia

I = b ⋅ h + 2 t 3 12 - b h 3 12 + t h 3 12

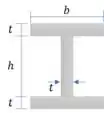
Aplicando os valores:

I = 200 ⋅ 199 3 12 - 200 ⋅ 175 3 12 + 12 ⋅ 175 3 12

I = 47,4 ⋅ 10 6   m m 4  

Passo 6

Vamos aplicar a equação da flexão:

σ a d m = M m á x c I

σ a d m = 0,55 ⋅ L 1 ⋅ W ⋅ h + 2 t 2 I

Isolando o peso W

W = 2 σ a d m ⋅ I 0,55 ⋅ L 1 ⋅ ( h + 2 t )

Aplicando os valores: W = 2 ⋅ 160   M P a ⋅ 47,4 ⋅ 10 6   m m 4 0,55 ⋅ 1,8   m ⋅ 199   m m

O resultado é:

W = 76,99   k N

Resposta

W = 76,99   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma viga composta é feita de madeira e duas chapas de aço, unidas com parafusos, como mostrado. Sabendo-se que os parafusos são de 16m m de diâmetro e espaçados longitudinalmente de 200m m , os módulo
Uma viga composta é feita de madeira e duas chapas de aço, unidas com parafusos, como mostrado. Sabendo-se que os parafusos são de 16m m de diâmetro e espaçados longitudinalmente de 200m m , os módulo
Uma barra de aço ( E a = 200G P a ) e uma de alumínio ( E a l = 70G P a ) são firmemente unidas para formar a viga composta mostrada. Para uma força cortante vertical de 20k N , determinar (a) a tensã
Uma viga composta é feita de madeira e duas chapas de aço, unidas com parafusos, como mostrado. Sabendo-se que os parafusos são de 16m m de diâmetro e espaçados longitudinalmente de 200m m , os módulo
Uma barra de aço ( E a = 200G P a ) e uma de alumínio ( E a l = 70G P a ) são firmemente unidas para formar a viga composta mostrada. Para uma força cortante vertical de 20k N , determinar (a) a tensã