Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 54b
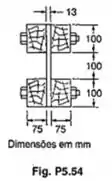
Uma viga composta é feita de madeira e duas chapas de aço, unidas com parafusos, como mostrado. Sabendo-se que os parafusos são de de diâmetro e espaçados longitudinalmente de , os módulos de elasticidade valem e , para o aço e para a madeira, repectivamente, e está sujeita a uma força cortante vertical de , determinar (a) a tensão de cisalhamento média nos parafusos (b) a tensão de cisalhamento no centro da seção transversal. (Sugestão: Usar o método indicado no prob. 5.52)
Passo 1
Vamos calcular o momento estático máximo na viga:
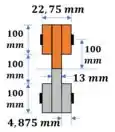
Passo 2
E agora é só calcular a tensão:
Resposta
Exercícios de Livros Relacionados
Quatro perfis de aço cantoneira 102 x 102 x 9,5 e uma placa de aço de 12 x 40 0m m são aparafusadas juntas para formar uma viga como a seção transversal mostrada. Os parafusos são de 22 m m de diâmetr
Resolver o Prob.5.40, considerando que a altura da placa é aumentada de 400m m para 600 m m .
Três pranchas são conectadas como mostrada, por parafusos de 16 m m de diâmetro e espaçados de 300m m , ao longo do eixo longitudinal da viga. Para uma força cortante vertical de 13350N , determinar a
Determinar a localização do centro de cisalhamento O de uma viga de parede fina de espessura uniforme e com a seção transversal mostrada.
Uma viga consiste em cinco pranchas de seção transversal 40x150 m m , conectadas por parafusos de aço, com espaçamento horizontal de 230m m . Sabendo-se que o cisalhamento na viga é vertical e igual a