Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 28
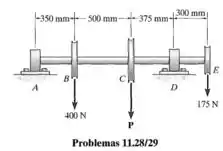
Trace os diagramas de força cortante e momento fletor para o eixo e determine, com aproximação de múltiplos de 5mm, o diâmetro exigido se e . Os mancais em A e D exercem somente reações verticais sobre o eixo. A carga é aplicada às polias em B, C e E. Considere P=550 N
Passo 1
A questão nos fornece os seguintes dados:
Começamos calculando as reações de apoio
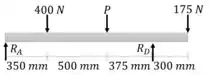
Passo 2
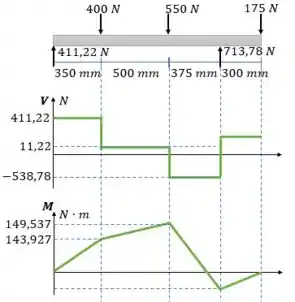
Passo 3
Vamos considerar que o eixo é maciço. Vamos então calcular o momento de inércia:
Passo 4
Vamos aplicar agora a equação da flexão:
Passo 5
Para testar a resistência sobre cisalhamento vamos calcular o momento estático máximo
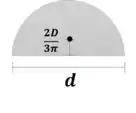
Passo 6
Agora vamos aplicar a equação do cisalhamento
Passo 7
Para garantir a resistência devemos escolher a maior dimensão:
Resposta
Exercícios de Livros Relacionados
Três placas de aço, cada uma com 12,5 mm de espessura, são soldadas juntas para formar uma viga em balanço. Para o carregamento mostrado, determinar as tensões normal e de cisalhamento nos pontos D e
Uma força de 12 kN é aplicada à extremidade livre da viga em balanço AB, na direção perpendicular ao eixo longitudinal da viga. Determinar a tensão no ponto A para quando o ângulo é 0 e para quando é
Uma força P de 5k N é aplicada a um arame, que é enrolado em torno da barra A B , como mostrado. Sabendo-se que a seção transversal da barra é um quadro de lado d = 40m m , determinar a tensão de cisa
Para a viga extrudada, com a seção transversal mostrada, determinar a localização do centro de cisalhamento O.
Para a viga extrudada, com a seção transversal mostrada, determinar a localização do centro de cisalhamento O.