Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 155
Um pedreiro estica uma corda entre dois pontos separados por 50 pés no mesmo nível com uma tensão de 10 libras em cada extremidade. Se a corda pesa 0,1 lb, determine a flexão h no meio da corda.
Passo 1
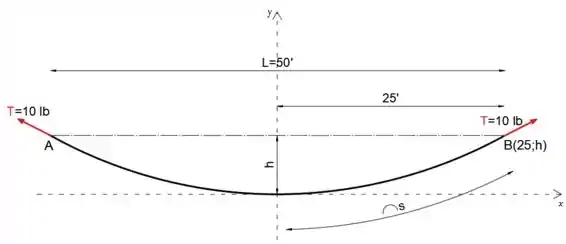
Primeiro, vamos desenhar o diagrama de corpo livre do cabo.
Observe que, uma vez que o cabo suporta apenas seu peso, o cabo tem uma forma conhecida como catenária
Podemos notar que a tensão no cabo é
Podemos ver no esboço que as coordenadas do ponto B são
Passo 2
Observe que o peso do cabo por comprimento é:
Onde o peso total é W = 0,1-lb e o comprimento total L = 2s
A partir daqui, podemos expressar como:
Usando a expressão , podemos escrever T0 como:
Substitua T e por seus valores
Passo 3
A seguir, usando a expressão (5/20), podemos determinar o comprimento s, uma vez que essa é a única incógnita na equação.
Substitua T0 e x por seus valores em pela expressão (1)
Passo 4
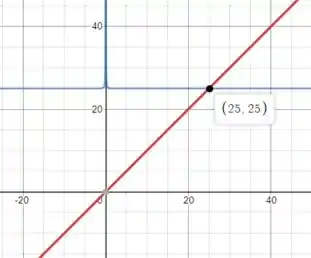
Usando uma calculadora gráfica como o Desmos (link nos comentários), traçaremos a função e e leia a solução do ponto de intersecção
Agora podemos calcular m da expressão (1)
Passo 5
Finalmente, para determinar o comprimento do afundamento, usaremos a expressão (5/19)
Substitua e T0 por seus valores e coloque as coordenadas do ponto B na equação