Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas de Revisão - Ex. 6
Localize o centroide do elemento.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta é uma questão basicamente de aplicação direto na fórmula. Precisamos determinar a área da superfície da correia em ao rotacionarmos a área sombreada em .
Como temos um sólido composto por alguns formatos (segmentos), vamos ter que calcular a área através da seguinte equação:
E agora vamos para as contas!
Passo 2
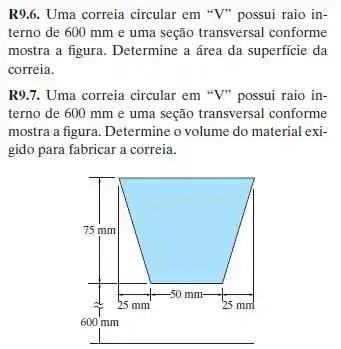
A nossa seção é composta por quatro partes: duas linhas horizontais (superior e inferior) e duas linhas inclinadas (a esquerda e a direita).
Relembrando, corresponde a distância perpendicular do eixo de rotação até o centroide de cada seção. Então, temos que identificar o seu valor para cada uma das partes analisadas.
Para as linhas horizontais, temos e . Já para as linhas inclinadas, temos e
Agora é só substituirmos os valores na fórmula! Portanto,
E assim finalizamos a questão!