Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas de Revisão - Ex. 4
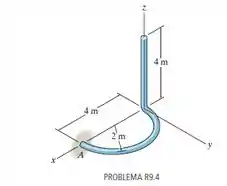
Localize o centroide do elemento.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos descobrir o centroide do elemento.
Para calcularmos essas medidas, basta lembrarmos das seguintes relações:
Então, vamos utilizar o bom e velho método de dividir para conquistar. Vamos dividir a nossa figura em duas seções. A primeira é o semicírculo no plano (segmento 1) e a segunda é a barra vertical no eixo (segmento 2).
Agora, vamos as contas!
Passo 2
Para nos auxiliar nas contas, vamos montar uma tabela com os valores do centroide e os respectivos produtos pela área (e embaixo o somatório).
Vejamos só abaixo:
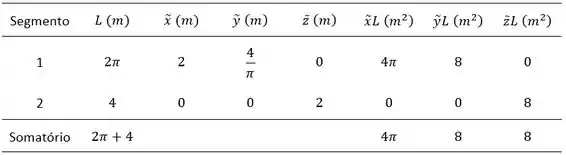
Então, as coordenadas do centroide são:
E assim finalizamos a questão!
Resposta
Exercícios de Livros Relacionados
Calcule as coordenadas do centro de massa do molde metálico fundido mostrado.
Determine a altura h da abertura retangular na placa quadrada, que resultará em um centro de massa, para o restante da placa, o mais próximo possível da borda superior.
Determine a profundidade h do furo circular no cubo, para a qual a coordenada z do centro de massa terá o maior valor possível.
Determine a profundidade h do furo circular no cubo, para a qual a coordenada z do centro de massa terá o maior valor possível.
Determine a coordenada y do centroide da área sombreada. Use o resultado do problema 5/41.