Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 53
Localize o centroide da área da seção transversal da viga construída.
Passo 1
Cara, fala aí! É o seguinte, a gente tem essa seção que é composta por várias figuras simples e ele quer a coordenada do centroide.
O que a gente pode fazer é dividir essa seção nessas figuras mais simples, calcular o centroide de cada uma, e suas áreas, e jogar na fórmulinha do centroide para regiões compostas:
Essa seção a gente vai dividir em quatro partes:
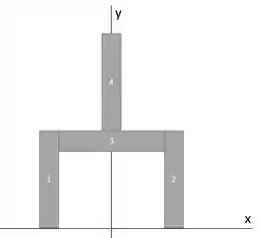
Passo 2
Todas essas figuras são retângulos, que têm seu centroide no seu centro. Vamos listar a área de cada um a coordenada do centroide de cada um em relação a mesma origem.
Vamos começar por (1) e (2).
Como nossa figura é simétrica: eles estão posicionados em relação a da mesma forma (repara, eles tem coordenada final e inicial iguais em ) e têm a mesma área, nós podemos determinar os valores apenas para (1) e multiplicar por 2 quando for jogar na fórmulinha.
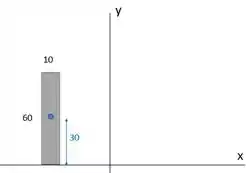
Passo 3
Agora vamos olhar para (3):
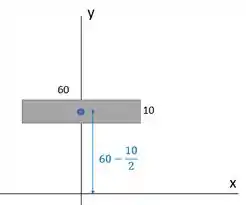
E para (4):
Passo 4
Nossa fórmulinha fica:
Substituindo os valores: