Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.10 - Ex. 206
Determine as coordenadas e do centroide da área sombreada.
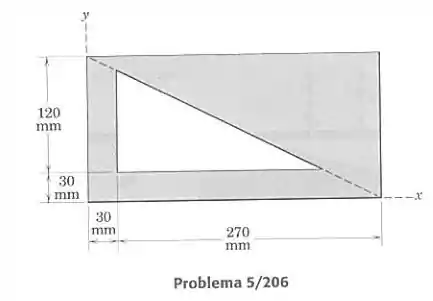
Passo 1
Aqui devemos achar os centróides do retângulo e do triângulo, e calcular as coordenadas do centroide da figura pela relação:
Essa é uma variação da fórmula para o calculo das coordenadas do centroide, na qual consideramos um espaço vazio como tendo umaárea negativa.
Passo 2
Pela simetria, o centroide do retângulo está em seu centro:
Sabe-se que a distância do centroide de um triângulo até um de seus lados, sendo a altura em relação a esse lado, é de . Devemos encontrar o tamanho dos catetos do triângulo para achar o centroide.
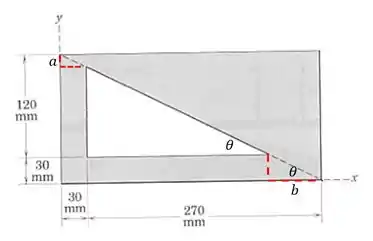
Achamos e através da tangente de que é a razão entre os lados do retângulo:
Então os lados do triângulo são:
E as coordenadas do centroide do tiângulo em relação ao sei vértice:
Mas como o vértice tem coordenadas (30, 30) mm:
Passo 3
Agora calculamos as áreas:
Passo 4
Finalmente, aplicamos nossa fórmula: