Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.10 - Ex. 218

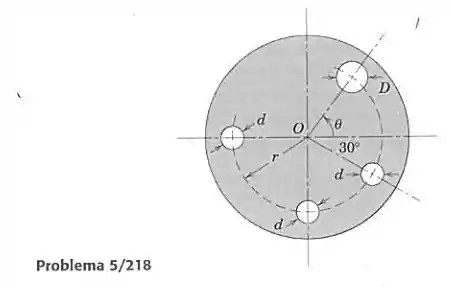
O disco circular gira em relação a um eixo que passa por seu centro O e tem três furos de diâmetro d , posicionados como mostrado. Um quarto furo deve ser usinado no disco, no mesmo raio r , tal que o disco estará em equilíbrio (centro de massa em O ). Determine o diâmetro necessário D do novo furo e sua posição angular.

Passo 1

Devemos fazer com que o centroide da área formada pelos 4 círculos seja no ponto O . Então vamos usar a fórmula do centroide combinado de várias áreas:

X - = A 1 x - 1 + A 2 x - 2 + A 3 x - 3 + A 4 x - 4 A 1 + A 2 + A 3 + A 4

Y - = A 1 y - 1 + A 2 y - 2 + A 3 y - 3 + A 4 y - 4 A 1 + A 2 + A 3 + A 4

Passo 2

A área dos círculos menores de diâmetro d é:

A 1 = A 2 = A 3 = π d 2 2 = π d 2 4

E as coordenadas de seus centros são:

x - 1 ,   y - 1 = - r ,   0

x - 2 ,   y - 2 = ( 0 ,   - r )

x - 3 ,   y - 3 = r cos ⁡ 30 ° ,   - r sen ⁡ 30 ° = 3 2 r ,   - r 2

Passo 3

Devemos ter X - = Y - = 0 . Então colocando na fórmula, primeiro para a coordenada x :

X - = 0 = A 1 x - 1 + A 2 x - 2 + A 3 x - 3 + A 4 x - 4 A 1 + A 2 + A 3 + A 4 = π d 2 4 - r + π d 2 4 0 + π d 2 4 3 2 r + A 4 x - 4 3 × π d 2 4 + A 4

O numerador então deve ser igual a zero:

- π d 2 r 4 + 3 π d 2 r 8 + A 4 x - 4 = 0

A área do nosso círculo será π D 2 4 , e sua coordenada x será r cos ⁡ θ :

- π d 2 r 4 + 3 π d 2 r 8 +   π D 2 r cos ⁡ θ 4 = 0

Agora dividimos tudo por π r e chegamos a nossa equação:

- d 2 4 + 3 d 2 8 + D 2 cos ⁡ θ 4 = 0

⇒ - 2 + 3 d 2 + 2 D 2 cos ⁡ θ 8 = 0 ⇒ D 2 cos ⁡ θ = 2 - 3 2 d 2

Passo 4

Vamos fazer a mesma coisa agora para a coordenada y . Dessa vez não vamos escrever o denominador, pois já sabemos que o que queremos é o numerador igual a zero:

0 = A 1 y - 1 + A 2 y - 2 + A 3 y - 3 + A 4 y - 4 = π d 2 4 0 + π d 2 4 - r + π d 2 4 - r 2 + A 4 y - 4

⇒ - π d 2 r 4 - π d 2 r 8 + A 4 y - 4 = 0

Substituindo A 4 = π D 2 4 e y - 4 = r sen ⁡ θ :

⇒ - 3 π d 2 r 8 + π D 2 r sen ⁡ θ 4 = 0

⇒ π D 2 r sen ⁡ θ 4 = 3 π d 2 r 8

Isolando D 2 sen ⁡ θ :

⇒ D 2 sen ⁡ θ = 3 π d 2 r 8 × 4 π r = 3 d 2 2

Passo 5

Encontramos nos passos 3 e 4 as seguintes relações:

D 2 cos ⁡ θ = 2 - 3 2 d 2

D 2 sen ⁡ θ = 3 d 2 2

Primeiro vamos obter θ . Dividindo a segunda pela primeira, temos:

D 2 sen ⁡ θ D 2 cos ⁡ θ = 3 d 2 2 2 - 3 2 d 2

⇒ tg ⁡ θ = 3 2 - 3 ≈ 11,2

⇒ θ = arctg ⁡ ( 11,2 ) = 84,9 °

Agora substituindo o ângulo na segunda relação:

D 2 sen ⁡ ( 84,9 ° ) = 3 d 2 2 ⇒ D 2 = 3 d 2 2 sen ⁡ 84,9 ° = 1,506 d 2

⇒ D = 1,227 d

Resposta

D = 1,227 d

θ = 84,9 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Localize o centro de massa ( x _ , y _ , z _ ) do bloco sólido homogêneo.
Determine o centro de massa ( x - , y - , z - ) do bloco sólido homogêneo.
Determine as coordenadas x e y do centroide da área sombreada.
Determine as coordenadas x e y do centroide da área sombreada.
Determine as coordenadas x,y e z do centro de massa do suporte feito de uma chapa metálica cuja espessura é pequena em comparação com as outras dimensões.