Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 38
Os mancais em A e D exercem somente as componentes y e z da força sobre o eixo. Se = 60 MPa, determine, com aproximação de 1 mm, o eixo de menor diâmetro que suportará a carga. Use a teoria da tensão de cisalhamento máxima.
Passo 1
Primeiramente, vamos determinar as forças atuantes e as reações de apoio. Sabemos que as reações mais distantes do ponto das forças serão a metade do ponto mais próximo, pois as distâncias são o dobro e temos que o somatório dos momentos tem que ser nulo. Caso fique confuso, basta fazer o somatório de forças em cada direção. Logo, fazendo o DLC, teremos:
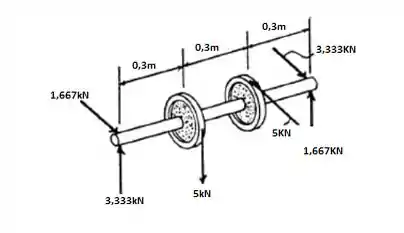
Vamos agora, determinar as forças atuantes em um dos pontos. Pegando o ponto B, teremos:
Calculando o momento fletor resultante, teremos:
Passo 2
Aplicando-se a teoria da tensão de cisalhamento máxima, temos que:
Substituindo os valores na fórmula, temos que:
Como teremos: