Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 108
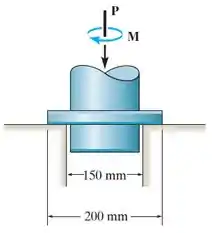
O mancal de escora suporta uniformemente uma força axial . Se um torque for aplicado ao eixo e fizer com que ele gire em velocidade constante, determine o coeficiente de atrito cinético na superfície de contato.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Temos que calcular o coeficiente de atrito cinético na superfície de contato de um mancal de escora.
Para a nossa alegria, a fórmula que relaciona o torque com este coeficiente de atrito já foi desenvolvida na seção 8.6! Então, temos apenas que aplicar a fórmula aqui.
Sendo assim, temos:
E assim finalizamos a questão!
Resposta
Exercícios de Livros Relacionados
A roldana dupla mostrada na figura é fixada a um eixo de 10m m de raio que se ajusta com folga a um mancal fixo. Sabendo que o coeficiente de atrito estático entre o eixo e o mancal pouco lubrificado
A roldana dupla mostrada na figura é fixada a um eixo de 10m m de raio que se ajusta com folga a um mancal fixo. Sabendo que o coeficiente de atrito estático entre o eixo e o mancal pouco lubrificado
Uma alavanca de peso desprezível está encaixada com folga em um eixo de 75m m de diâmetro. Observa-se que a alavanca apenas inicia um movimento de rotação se a massa de 3k g é adicionada em C . Determ
Uma alavanca A B de peso desprezivel é montada com folga em um eixo fixo de 63m m de diâmetro. Sabendo que o coeficiente de atrito estático entre o eixo fixo e a alavanca é 0,15 ; determine P necessár
Resolva o Problema 8.90 considerando que a força normal por unidade de área entre o disco e o assoalho varia linearmente desde um máximo no centro até zero na circunferência do disco.