Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 95
Resolva o Problema considerando que a força normal por unidade de área entre o disco e o assoalho varia linearmente desde um máximo no centro até zero na circunferência do disco.
Passo 1
Bom galera, começamos já sabendo que:
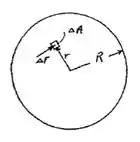
E como tempos a força:
Logo ficamos com:
Passo 2
Show de bola, a força normal é dada por:
Logo podemos ter:
Passo 3
Então, o momento total fica:
Passo 4
Por fim, a gente aplica o que a gente tem no que encontramos:
Substituindo fica:
E pronto, temos que:
Resposta
Exercícios de Livros Relacionados
O cilindro de massa m está preso ao anel A , que está suspenso pelo cabo que passa sobre a polia, como mostrado na parte a da figura. Um momento M aplicado à polia a faz girar até que ocorre deslizame
O projeto de uma chave de correia para soltar filtro de óleo está mostrado na figura. Se o coeficiente de atrito entre a correia e o filtro vale 0,25, determine o valor mínimo de h que assegura que a
A correia sem fim de uma escada rolante passa em volta do tambor esticador A e é movimentada por um torque M aplicado ao tambor B . A força trativa na correia é ajustada por um esticador em C , que pr
A viga em I uniforme tem uma massa de 74 kg por metro de comprimento e é suportada por uma corda que passa sobre o eixo fixo de 300 mm. Se o coeficiente de atrito entre a corda e o eixo vale 0,5, calc
Encontre o momento M necessário para girar o tubo no bloco em V contra a ação da cinta flexível, no projeto do freio de cinta mostrado. Uma força P = 100N é aplicada à alavanca, que pivota em torno de