Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas - Ex. 1
Determine o centro de massa do elemento homogêneo encurvado na forma de um arco circular.
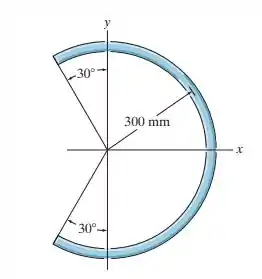
Passo 1
Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão de Estática.
Para determinarmos o centroide deste elemento curvo, devemos determinar o elemento diferencial. Como estamos trabalhando com um contorno circular, o elemento diferencial está localizado sobre a curva no ponto arbitrário :
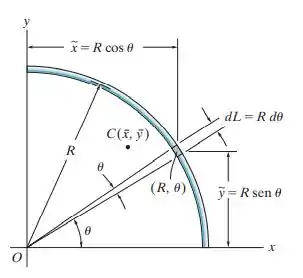
devemos utilizar coordenadas polares. Assim, escolhemos o elemento na forma triangular. Fica assim:
Primeiro, vamos determinar a componente . Ela é dada por:
Substituindo:
Passo 2
Agora, para determinarmos a posição do centro de massa, podemos utilizar o conceito de simetria do elemento neste eixo. Portanto:
É isso, galera, Bora resolver mais questões pra ficar craque.