Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 84
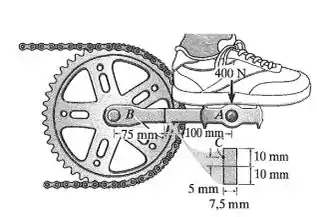
A manivela do pedal de uma bicicleta tem a seção transversal mostrada na figura. Se ela estiver presa à engrenagem em B e não girar quando submetida a uma força de 400 N, determine as tensões principais no material na seção transversal no ponto C.
Passo 1
Fala, meu querido!
Mas essa situação tá bem confusa, né? O que está acontecendo ali, vamos pensar. AB é uma manivela. Vamos pensar nela como uma barrinha. Se houver força de em , essa barrinha não gira. Isso quer dizer que gera reações nessa barrinha para ela não girar.
Basicamente, temos uma barrinha com uma força de na extremidade, e reações na outra extremidade.
E é um ponto dentro dessa manivela onde a gente tem que achar as tensões.
Aqui temos um ponto em uma seção sujeita a esforços internos. O que ele quer de nós é que a gente ache as tensões principais nesse ponto.
Como a gente faz isso? Cara, a gente vai achar as tensões nesse ponto e depois vai usar o círculo de Mohr para achar o valor das tensões principais. Vai ser lindo! Vem comigo!
Passo 2
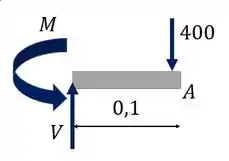
Primeiramente, vamos calcular os esforços atuantes na seção que contem Vamos cortar nossa barra nessa seção e achar os esforços por equações de equilíbrio.
Passo 3
Esse ponto sofre tração causada pelo momento. Aí nossa fórmulinha para a tensão normal fica:
Mas repara que é o momento de inercia em relação ao eixo horizontal da nossa seção. E é a distância de até esse eixo, então .
Ficamos assim:
Como temos um esforço cortante, teremos cisalhamento.
O vai ser o mesmo da outra fórmulinha. vai ser a espessura da nossa seção, . E vai ser o momento estático da área acima da linha que passa por .
Temos então
Prontinho, achamos as tensões.
Passo 4
Agora vamos montar nosso círculo de Mohr. Precisamos de umas coisinhas.
A tensão média:
Ela é a média das tensões normais que a gente achou em diferentes direções. Uma foi e a outra é zero mesmo.
E o raio do círculo:
A gente pode substituir nossa tensão em ou . Depende do referencial. O importante é que uma seja zero e outra seja ;
Agora vem a parte interessante. Como ele só pede o valor das tensões principais, não precisamos desenhar o círculo, só lembrar que por ele:
Logo, podemos calcular as tensões principais:
Uhul! Arraso!