Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 93

Um membro em compressão de 3m de comprimento efetivo é feito, aparafusando-se juntos dois perfis laminados de aço L 102 × 76 × 6,4 , como mostrado. Sabendo-se que σ e = 250   M P a   e   E = 200 G P a , determinar a carga centrada admissível para este membro comprimido.

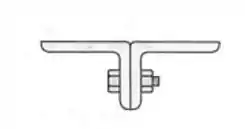
Passo 1

E ai gurizada tudo bem? O enunciado pede que a gente determine a carga centrada admissível para este membro comprimido. Partiu?

Aço: C c = 2 π 2 E σ y = 2 π 2 200 × 10 9 250 × 10 6 = 125,66

Considere que:

L 127 × 76 × 12,7 m m        

Mesa dispôe A L = 2420 m m 2 ,     I x = 3,93 × 10 6 m m 4

y = 44,4 m m ,     I y = 1,06 × 10 6 m m 4 ,       x = 19,0 m m ,     r y =

Para a coluna

I x = 2 I y m e s a = 2 1,06 × 10 6 = 2,12 × 10 6 m m 4

I y > I x       I m i n = I x = 2,12 × 10 6 m m 4 = 2,12 × 10 - 6 m 4

Passo 2

Calcule a área agora, vem comigo :D

A = 2 A , = 4840 m m 2 = 4840 × 10 - 6 m 3

r = I m i n A = 2,12 × 10 - 6 4840 × 10 - 6 = 20,93 × 10 - 3 m

Temos a razão comprimento / raio:

L e r = 2,3 20,93 × 10 - 3 = 109,90 < C c   L e r C c = 0,87455

O fator de segurança é dado por:

F . S . = 5 3 + 3 8 0,87455 - 1 8 0,87455 2 = 1,9110

σ μ = σ x 1,9110 1 - 1 2 L r C c 2 = 250 × 10 6 1,9110 1 - 1 2 0,87455 2 = 80,79 × 10 6 P a

P μ = σ μ A = 80,79 × 10 6 4840 × 10 - 6 = 391 × 10 3 N = 391 k N

Resposta

391 k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um membro em compressão tem a seção transversal mostrada e um comprimento efetivo de 2m. Sabendo-se que a liga de alumínio usada é 2014-T6, determinar a carga centrada admissível.
Um membro em compressão de comprimento efetivo igual a 9 m é obtido soldando-se duas placas de aço de 10 mm de espessura a um perfil laminado de aço w250 x 80, como mostrado. Sabendo que σ= 320 MPa e
Resolver o problema 11.100 assumindo que o comprimento efetivo do membro comprimido é aumentado para 2,75 m.
Um membro em compressão de comprimento efetivo igual a 9 m é obtido soldando-se duas placas de aço de 10 mm de espessura a um perfil laminado de aço w250 x 80, como mostrado. Sabendo que σ= 320 MPa e
Um membro em compressão tem a seção transversal mostrada em um comprimento efetivo de 1,5m. Sabendo-se que a liga de alumínio usada é 6061 - t 6 , determinar a carga a carga centrada admissível.