Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática - 12ªEd- Ed: 14º - Capítulo 5.Problemas - Ex. 74
O membro está fixado em e por mancais radiais lisos. Determine as componentes das reações nesses mancais se o membro estiver submetido à força . Os mancais estão no alinhamento apropriado e exercem apenas reações de força sobre o membro.
Passo 1
Oi, tudo bem? Vamos analisar esta questão.
Vamos encontrar os valores das componentes de já que sabemos que sua intensidade vale . Temos que:
E:
Agora devemos construir um diagrama de corpo livre separando cada componente tanto da força quanto das reações de apoio em , e . Temos que:
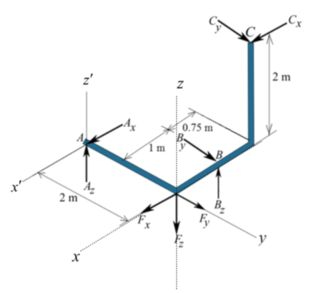
Fazendo o somatório de momento em , temos que:
Fazendo o somatório de momento em , temos que:
Fazendo o somatório de momento em , temos que:
Passo 2
Vamos analisar agora o equilíbrio ao longo de . Temos que:
O equilíbrio ao longo de :
E o equilíbrio ao longo de :
Passo 3
Temos incógnitas e equações, então podemos resolver este sistema.
Vamos substituir em . Teremos que:
Agora vamos substituir em . Teremos que:
Subtraindo as duas equações encontradas, temos:
Portanto:
Passo 4
Faremos esse processo de manipulação das equações até encontrar todos os valores desconhecidos.
Sabemos que:
Portanto:
E:
Logo:
Passo 5
Temos que:
Logo:
E:
Logo:
As componentes de cada ponto que não foram mencionadas, são nulas.