Como parte de uma verificação de seu projeto, o braço inferior de suspensão (parte da suspensão de um automóvel) é sustentado por mancais em e e submetido ao par de forças de em e . A mola da suspensão, não mostrada para melhor clareza da figura, exerce uma força em , como mostrado, onde está no plano . Determine o módulo da força da mola e os módulos e das forças dos mancais em e , que são perpendiculares ao eixo da dobradiça.
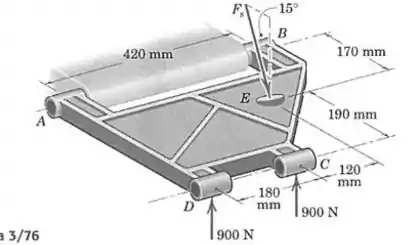
Passo 1
Primeiro vamos definir os nosso eixos:
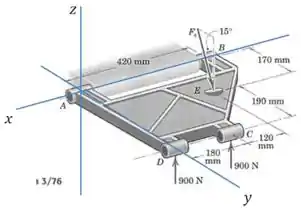
E as forças atuando no sistema são as seguintes: as duas forças de em e , a força da mola, e as forças e que queremos calcular.
Como o enunciado diz que essas duas forças são perpendiculares ao eixo , sabemos que elas não tem nenhuma componente no nosso eixo , ou seja:
E a força também pode ser escrita na forma vetorial:
Não vamos desenhar todas essas componentes no desenho para evitar uma confusão, mas elas são fáceis de imaginar por serem paralelas aos eixos , e .
Passo 2
Ok, agora vamos analisar as condições de equilíbrio. Os momentos precisam ser nulos em relação a todos os eixos:
Olhando para a figura vamos escrever as expressões para cada um desses momentos.
Todas as forças em e têm momento nulo em relação a , porque seus pontos de aplicação estão sobre esse eixo. Então só escrevemos os momentos das duas forças de e de uma componente da força .
Dessa vez as componentes da força e uma das forças de estão sobre o eixo, e é paralela a ele.
E agora é só seguir a mesma lógica para escrever :
Passo 3
Ótimo, agora vamos organizar isso tudo em um sistema:
Substituindo a primeira equação nas duas últimas:
Ok, já encontramos as componentes da força e a força .
Passo 4
Vamos usar a condição de equilíbrio das forças para encontrar a força , isso é bem mais simples do que analisar os momentos.
Na direção do eixo temos as seguintes forças:
E na direção do eixo :
E substituindo os valores ficamos com um sistema bastante simples:
E então:
Agora só falta calcular os módulos das duas forças e :
Resposta
As forças são , e .