Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 114

Uma placa circular horizontal de peso igual a 267 N é suspensa por três fios que são ligados a um suporte D e formam ângulos de 30° com a vertical. Determine a tração em cada fio.

Passo 1

Vamos começar desenhando o diagrama de corpo livre da placa:

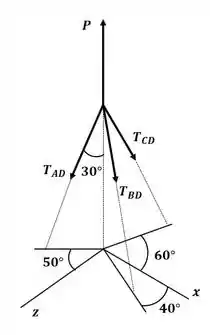
Passo 2

Agora vamos aplicar as equações de movimento para o sistema, começando com o somatório de forças em :

Simplificando a expressão, temos:

Essa será nossa equação 1. Agora aplicando o somatório de forças na direção :

Simplificando a expressão, temos:

Essa será nossa equação 2. Agora aplicando o somatório de forças na direção :

Simplificando a expressão, temos:

Essa será nossa equação 3.

Passo 3

Agora, isolando da terceira equação:

E, susbtituindo esse valor na equação 1 e 2:

E, substituindo a expressão encontrada para nessa última equação, temos:

Substituindo esse valor na equação anterior:

Agora, substituindo esses dois valores na segunda equação 2:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A laje de concreto uniforme tem massa de 2400k g . Determine a tração em cada um dos três cabos de apoio paralelos quando a laje é mantida no plano horizontal, conforme mostrado na figura.

O carrinho sustenta o engradado uniforme com massa de 85k g . Determine as reações verticais sobre os três rodízios em A ,B e C . O rodízio em B não aparece na figura. Despreze a massa do carrinho.

O membro é sustentado por um eixo retangular que se encaixa livremente no furo retangular liso da luva conectada em A e por um rolete em B. Determine as componentes de reação desses apoios quando o me

A carga uniforme tem massa de 600 kg e é levantada usando uma viga uniforme de 30 kg BAC e quatro cordas, como mostra a figura. Determine a tração em cada corda e a força que precisa ser aplicada em A

A plataforma tem massa de 3 Mg e centro de massa localizado em G. Se ela for elevada com velocidade constante usando três cabos, determine a força em cada um desses cabos.