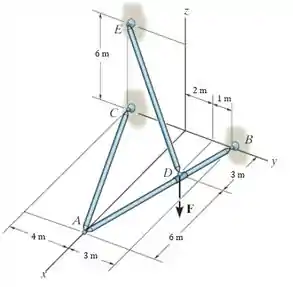
A estrutura de três membros é conectada em suas extremidades por meio de juntas esféricas. Determine as componentes da reação em e a tração no membro . A força agindo em é .
Passo 1
Vamos desenhar o diagrama de corpo livre do trecho , beleza?
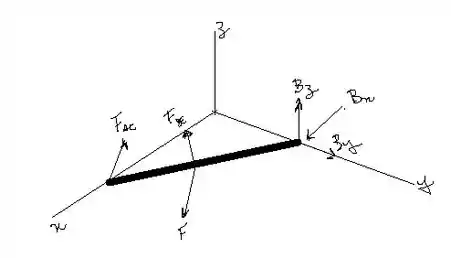
Antes de seguirmos com o cálculo de momentos e forças, vamos olhar para dois triângulos: os . Vamos olhar primeiro para o triângulo . Dele nós podemos tirar o valor da hipotenusa através do teorema de Pitágoras. Assim,
Agora que temos o valor de , podemos encontrar o valor da hipotenusa do triângulo !
Tendo o valor da hipotenusa podemos escrever o valor dos cosseno e seno:
Passo 2
Para um corpo em equilíbrio, tanto o somatório dos momentos quanto o somatório das forças são iguais a zero. Assim, calculando o momento em relação aos eixos e adotando como sentido positivo o anti-horário para o momento e para cima e para direita para as forças, temos:
Resposta
As forças são: